Material of the Examples (supplementary)
Chapter: A Computational Model of the Mind: How to Think about Complex Systems in Nature Springer Nature, Integrated Science Series, 2023; Integrated Science book series (IS,volume 12), 553 - 573 - ISBN: 978-3-031-15958-9
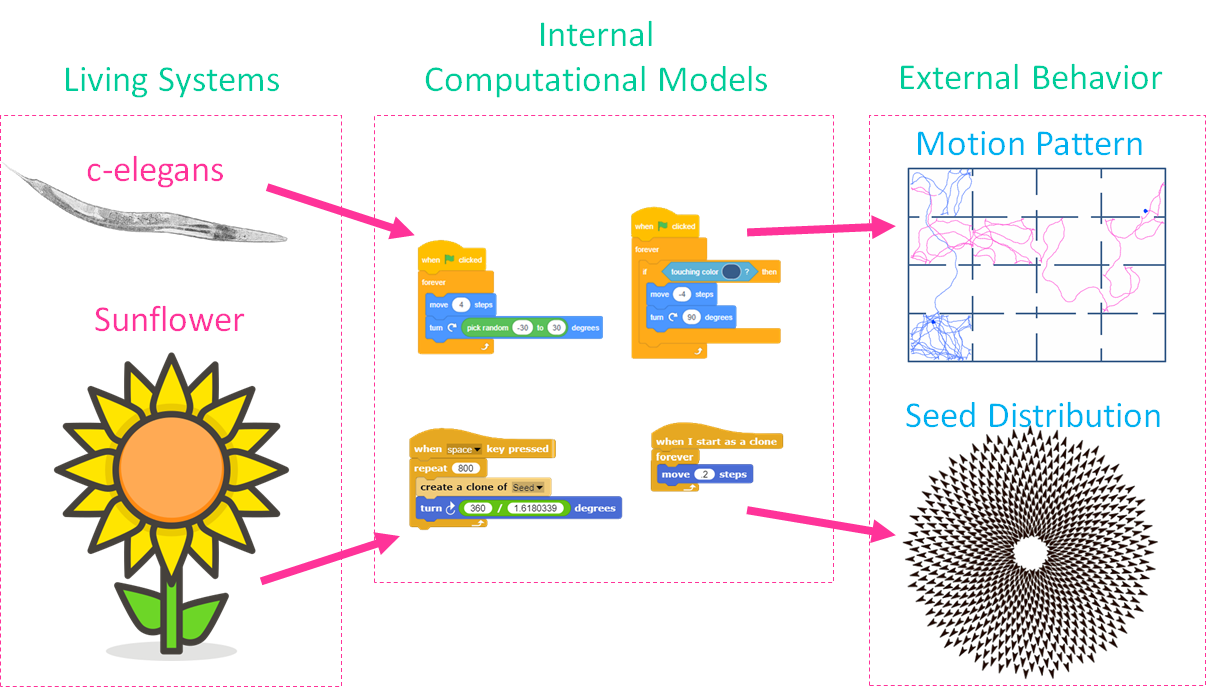
Example1: c-elegans
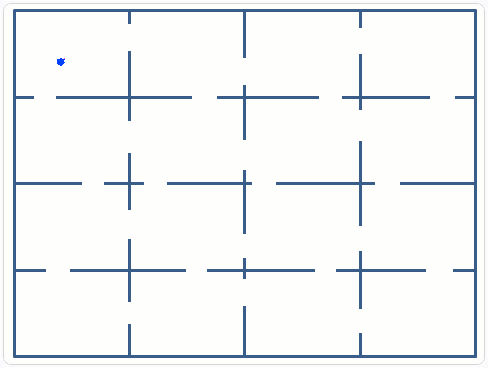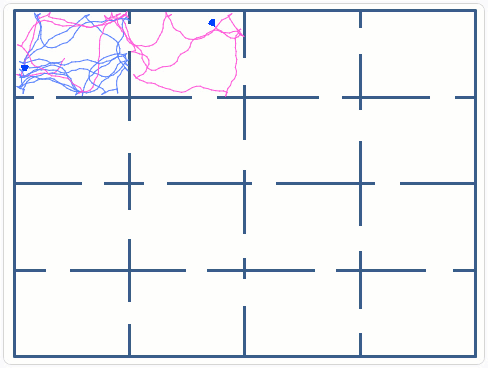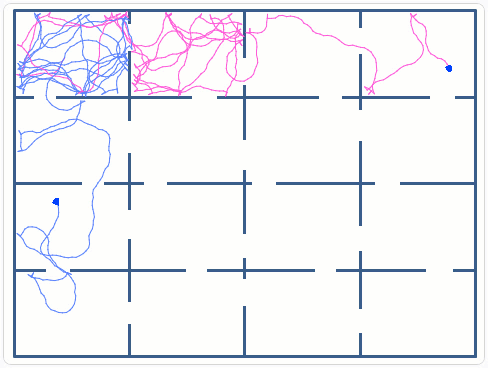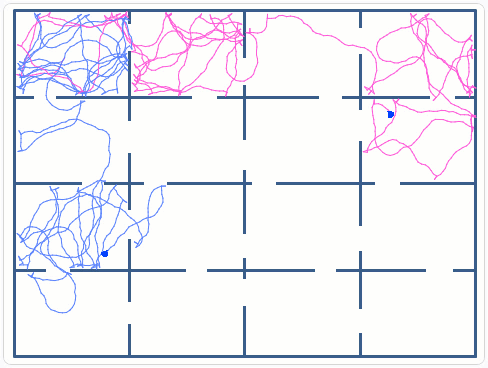
Simulation of the motion patterns of the c-elegans worm with the objective to relate simple neural activity and complex behavioral patterns.
These simulations allow us to visualize the complex external behavior created by a simple control system. It also allows the probabilistic study of parameter sets of the controls, and how these affect the overall performance:
- Is it possible to find all 16 compartments of the maze is a given time period?
- What are the tradeoffs between speed and collision? Etc.
The numerical values of the forward motion, 4 steps, and the random turns, +/- 30 degrees, were determined by trial and error.
In addition, by simulating multiple c-elegans with different sets of parameters, one could compare their performance, and in a process analogous to evolution by natural selection, select those that outperformed their competitors.
Example 2: Sunflower

The study of the complex distribution of the sunflower seeds and its relationship with two concepts: the Fibonacci sequence, and the golden ratio.
Computational system that distributes 800 seeds in a pattern the replicates natural sunflowers. The complete control includes only two scripts.
- The script on the left creates in a loop 800 distinct seeds. The only relevant process is that after one seed is created, a simple rotation of 360/1.61803 degrees is implemented, and the process of creation and rotation is repeated. The expression is presented in this form for clarity, to signify that the turn is a complete circle divided by the golden ratio. This first script distributes the stems from which the seeds will grow.
- The second script, which even simpler, is the pattern of movement of each seed after it has been created. The motion is a simple constant forward movement. One can think that this motion represents the motion of each stem as it is pushed outward when the seeds grow in size.
All seeds are created at the center of the flower. The orientation of each seed is determined by a turn of 222.5 degrees (360/golden ratio) from the previous seed.
Example 3: Pandemic

The simulation of the complex patterns in the dynamics of a pandemic using a small set of computational systems based on the intuitive ideas of how pandemics surge, extend, contract and disappear.
We will represent a community of 100 citizens under study as a set of 100 circles that may freely move on a stage that represents their community. We will color code the citizens in order to represent their health status: blue means healthy, pink means infected, and green means recovered.
Initially, 99 citizens will have a healthy status, blue color.
One of the citizens will be infected with the virus, pink color.
As the citizens move about their town, they may get in contact with each other. In that case, a healthy citizen will become infected by the virus if the contact is with a carrier person. From the moment a citizen becomes infected, it enters a period of recovery, and its status is changed to pink color. After the period of recovery is completed, the health status changes to recovered: green color.
The simulation includes an orange graph that represents the total number of infected citizens throughout the period of pandemic.
One of the parameters that is studied in this simulation is the percentage of citizens that is required to be in confinement (stay-at-home.) By changing the value of this parameter, the simulation will reflect the corresponding evolution, orange graph, of the number of infected people at any time.
Graphical Abstract
The collaboration between the areas of computation and the biological sciences in the last two decades has changed in essential ways the scope and methods of research in their shared field.
In this chapter we describe two fundamental principles: Computational Equivalency; and the Suboptimal Paradigm of Evolution. These principles permeate current research in computation and biology.
We illustrate these principles with three examples: animal behavior; plant behavior; and human interaction. These examples are described formally by means of computational languages.
These descriptions are designed to provide the reader with a concrete framework where these and similar ideas could be studied, tested, and developed. The computational descriptions of these systems are simple and easily accessible to readers. This accessibility makes appropriate the introduction of these ideas in the traditional school curriculum. Our current students are the future custodians of our society. They need novel ideas to respond to the novel challenges of the modern society.
All programs referenced in this chapter are accessible in the links provided in this webpage. In addition, these links include animations of their dynamic processes.

