1.- ¿Qué datos necesitamos para generar los difractogramas?



Un análisis de los modelos estructurales de estos tres minerales pone de manifiesto la similitud que presentan:
- Sus parámetros de celda tienen valores muy semejantes.
- Cristalizan en el mismo sistema cristalino y grupo espacial: Trigonal, R-3c.
- Los átomos dentro de la celda unidad se sitúan en las mismas posiciones: sus coordenadas son semejantes.
La diferencia más importante que podemos apreciar es la composición química de cada mineral: la calcita contiene Ca, la magnesita Mg y la siderita Fe. Este es un buen ejemplo de minerales isoestructurales*. Como sabemos, la fórmula de la calcita es Ca(CO3), por lo que la magnesita y la siderita tendrán fórmulas químicas análogas:
| Mineral | Fórmula |
| calcita | Ca(CO3) |
| magnesita | Mg(CO3) |
| siderita | Fe(CO3) |
[Arriba]
2.- ¿Cómo generamos los difractogramas de rayos X?
Creemos los ficheros de entrada al programa PowderCell de los tres minerales con la información necesaria para simular sus diagramas de difracción (ver la sección de Recursos dedicada PowderCell para más detalles).
Fichero calcita.celCELL 4.9900 4.9900 17.002 90. 90. 120.
Ca1 CA 0.00000 0.00000 0.00000 1.00000 0.00000
C1 C 0.00000 0.00000 0.25000 1.00000 0.00000
O1 O 0.25780 0.00000 0.25000 1.00000 0.00000
RGNR 167
Fichero magnesita.cel
CELL 4.633 4.633 15.016 90. 90. 120.
Mg1 MG 0.00000 0.00000 0.00000 1.00000 0.00000
C1 C 0.00000 0.00000 0.25000 1.00000 0.00000
O1 O 0.27760 0.00000 0.25000 1.00000 0.00000
RGNR 167
Fichero siderita.cel
CELL 4.6887 4.6887 15.373 90. 90. 120.
Fe1 FE 0.00000 0.00000 0.00000 1.00000 0.00000
C1 C 0.00000 0.00000 0.25000 1.00000 0.00000
O1 O 0.27430 0.00000 0.25000 1.00000 0.00000
RGNR 167
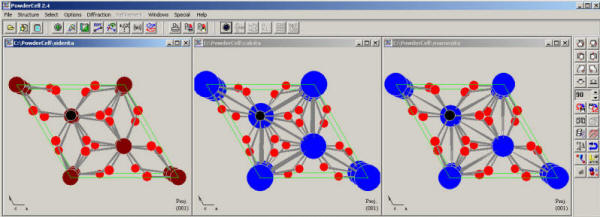
Como hemos venido haciendo en los ejemplos guiados anteriores, ejecutamos PowderCell para representar la estructura de estos minerales. Abrimos los tres ficheros con extensión .cel de forma sucesiva para poder comparar sus estructuras cristalinas. Tras ejecutar el comando {Windows -> Tile} para poder ver simultáneamente las tres estructuras, el aspecto de la ventana principal será:
|
|
||
| siderita | magnesita | calcita |
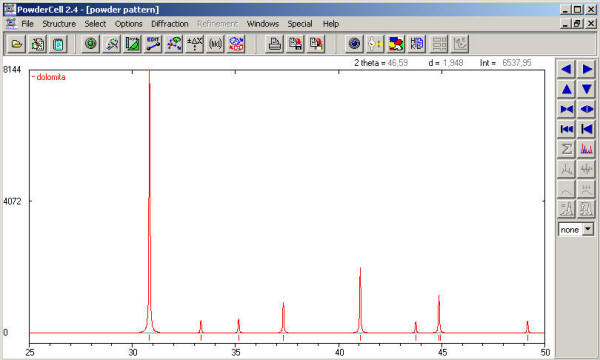
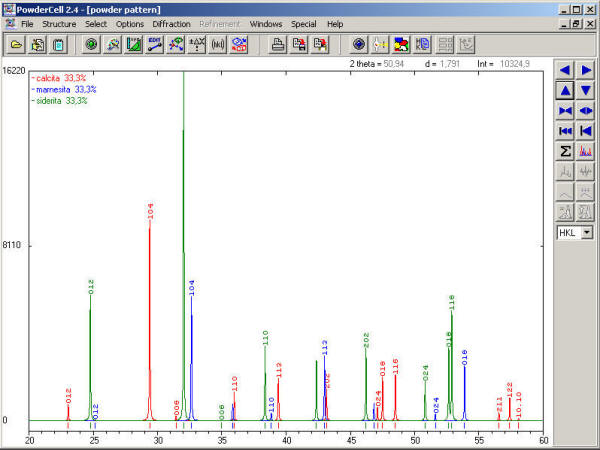
Pinchando en el icono nº 11 se activa la ventana que nos muestra los difractogramas de rayos X de la calcita, magnesita y siderita. En la siguiente imagen se ha seleccionado la región del difractograma comprendida entre 20º a 60º (ver Ejemplo B para más detalles) y se ha maximizado la ventana para una mejor visualización de los máximos de difracción.
[Arriba]
3.- ¿Qué relación existe entre los difractogramas?
Sin embargo, los difractogramas de los tres minerales muestran diferencia apreciables, a pesar de presentan máximos de difracción con los mismos índices de Miller (hkl): la posición y la intensidad de los máximos varían de unos minerales a otros.
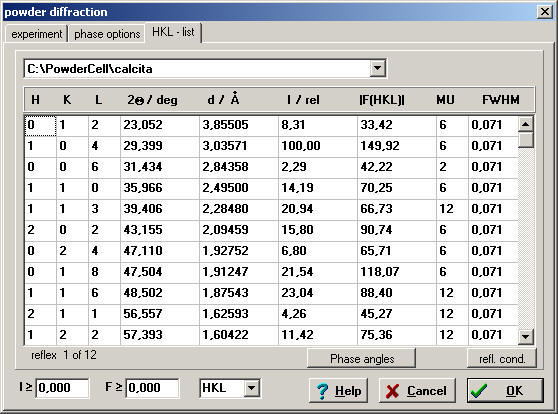
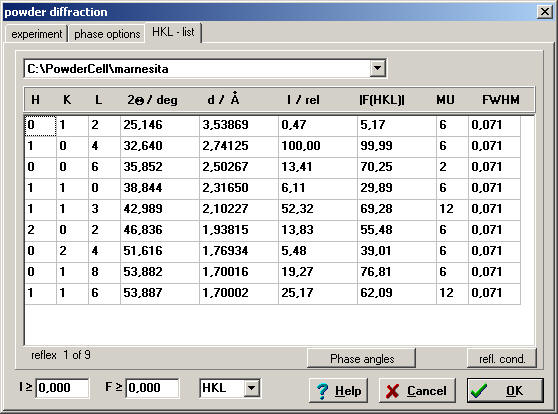
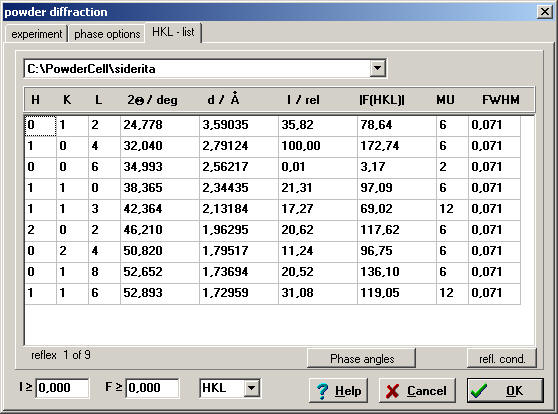
Esto se debe a que el radio iónico* de los metales Ca, Mg y Fe es diferente, por lo que el tamaño de la celda también debe serlo para que puedan alojarse átomos que ocupan distinto volumen. Por ello, a mayor radio iónico del metal mayor será el espaciado reticular de una determinada familia de planos reticulares (hkl). Veamos como ejemplo como varía la posición del máximo de difracción (104) de mayor intensidad:
| Mineral | Fórmula | Radio iónico (Å) |
Espaciado reticular d(104)(Å) |
| calcita | Ca(CO3) | 1.00 | 3.03571 |
| siderita | Fe(CO3) | 0.78 | 2.79124 |
| magnesita | Mg(CO3) | 0.72 | 2.74125 |
[Arriba]
4.- ¿Qué difractograma generará un mineral de composición química intermedia entre otros dos?
La calcita, Ca(CO3), y la magnesita, Mg(CO3), son los términos extremos de la solución sólida de fórmula general (Ca,Mg)CO3. Vamos a simular su difractograma y compararlo con el de la calcita y el de la magnesita. La primera entrada tras buscar dolomite en la base de datos AMCSD es la siguiente:

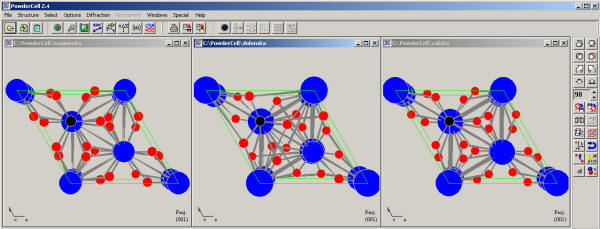
Por razones que superan los objetivos de esta práctica guiada, el modelo estructural de la dolomita se describe con el grupo espacial R-3 en lugar de el utilizado para la calcita y la magnesita, R-3c. Este detalle no debe confundirnos, pues la dolomita sigue siendo isoestructural con ambos minerales. Podemos comprobarlo realizando la representación gráfica de su estructura.
Fichero dolomita.cel
CELL 4.815 4.815 16.119 90.0 90.0 120.0
Ca1 CA 0.00000 0.00000 0.00000 1.00000 0.00000
Mg1 MG 0.00000 0.00000 0.50000 1.00000 0.00000
C1 C 0.00000 0.00000 0.24350 1.00000 0.00000
O1 O 0.23740 0.96530 0.24400 1.00000 0.00000
RGNR 148
|
|
||
| magnesita | dolomita | calcita |
Lógicamente, los máximos de difracción de la dolomita deben encontrarse entre los máximos análogos de la calcita y la magnesita. Si representados sus difractogramas lo podremos apreciar.
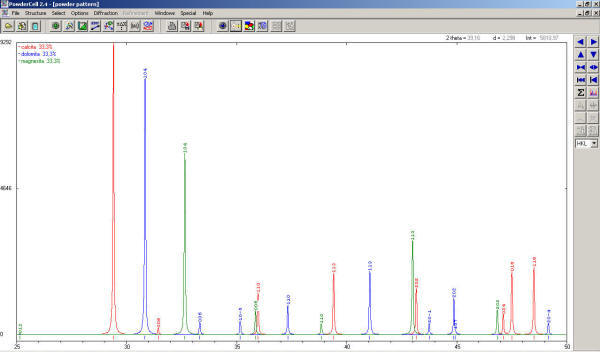
[Arriba]
5.- ¿Qué diferencia existe entre una mezcla de fases y una solución sólida?
Para responder a esta pregunta debemos recordar que una mezcla de fases, por ejemplo las fases A y B, generarán un difractograma suma A+B de los difractogramas individuales de cada fase (ver apartado 4 del Ejemplo B).
Sin embargo, una fase C de composición química intermedia entre A y B y con su misma estructura cristalina poseerá su propio difractograma que lo identifica como una fase distinta a las anteriores.
En un experimento de difracción, ambos casos pueden identificarse sin dificultad. Sus difractogramas simulados serían:
Mezcla de calcita, Ca(CO3), y
magnesita, Mg(CO3), en iguales proporciones
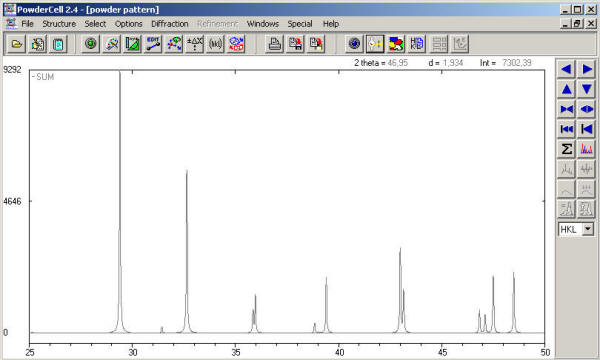
Dolomita, (Ca0.5Mg0.5)CO3