1.- ¿Qué datos necesitamos para generar los difractogramas?
En primer lugar debemos hacer la búsqueda de los datos cristalográficos de los minerales calcita y aragonito: parámetros de celda, grupo espacial y coordenadas atómicas. Para ello, nos ayudaremos de la base da datos AMCSD. En este caso, los dos minerales son polimorfos*, por lo que vamos a utilizar como criterio de búsqueda los elementos químicos que aparecen en sus fórmula, Ca(CO3).
Tras conectarnos a Internet y acceder a la base de datos, tenemos que pinchar en Chemistry Search. En la Tabla Periódica que nos aparece seleccionaremos los elementos que nos interesan: Ca, C y O. Además, para restringir más la búsqueda, excluiremos el resto de los demás elementos químicos (Exclude Others). Para saber más acerca de como realizar las búsquedas en esta base de datos, visita en la sección recursos la página dedicada a AMCSD.
El resultado de la búsqueda es de 12 entradas. Las dos primeras que aparecen son las que vamos a utilizar y las que a continuación se muestran.

Debes guardar la información cristalográfica de cada mineral en ficheros separados (como se ha indicado en el Ejemplo guiado A). Posteriormente utilizaremos esta información para simular los diagramas de rayos X en muestra policristalina correspondientes a ambas fases con el programa PowderCell.
[Arriba]
2.- ¿Cómo podemos generar los difractogramas de rayos X?
En primer lugar debemos crear los ficheros de entrada calcita.cel y aragonito.cel que puedan ser leídos por el programa PowderCell. Recordad que debemos crearlos con el bloc de notas y que cada uno de ellos tiene que contener la siguiente información:
- línea 1: CELL seguido de seis numérico reales correspondientes a los parámetros de celda a, b, c, a, b, g.
-
línea 2 y sucesivas: Cada línea se dedica a la
información
de cada átomo de la unidad asimétrica. Se debe suministrar:
- Nombre del átomo (una etiqueta para identificarlo).
- Especie atómica (código de la tabla periódica).
- Tres números reales correspondientes a las coordenadas x, y, z del átomo.
- Un número entero correspondiente al factor de ocupación del átomo (generalmente 1.0)
- Un número entero correspondiente al factor de temperatura del átomo (generalmente 0.0). - línea final: RGNR seguido del número del grupo espacial en el cristaliza el mineral.
Los dos ficheros de entrada al programa PowderCell generados de esta manera se presentan a continuación:
Fichero calcita.cel
CELL 4.9900 4.9900
17.0615 90. 90. 120.
Ca1 CA 0.00000
0.00000 0.00000 1.00000 0.00000
C1 C 0.00000
0.00000 0.25000 1.00000 0.00000
O1 O 0.25780 0.00000 0.25000
1.00000 0.00000
RGNR 167
Fichero aragonito.cel
CELL 4.9614 7.9671 5.7404 90. 90. 90.
Ca1 CA 0.25000 0.41500 0.75970
1.00000 0.00000
C1 C 0.25000 0.76220 -0.08620
1.00000 0.00000
O1 O 0.25000 0.92250 -0.09620
1.00000 0.00000
O2 O 0.47360 0.68100 -0.08620
1.00000 0.00000
RGNR 62
Queremos estudiar la relación que existe entre los difractogramas de dos compuestos polimorfos, la calcita y el aragonito. Para ello, leeremos estos ficheros con el programa PowderCell {File –> Load} o pinchando en el icono número 1. Seleccionaremos uno de los dos ficheros que nos interesa, por ejemplo calcita.cel. Repetiremos este proceso con el segundo fichero, aragonito.cel. Nos aparecerán en la pantalla las representaciones de ambas estructuras cristalinas. Para verlas sin que se superpongan, ejecuta el comando {Windows -> Tile}. El resultado será:
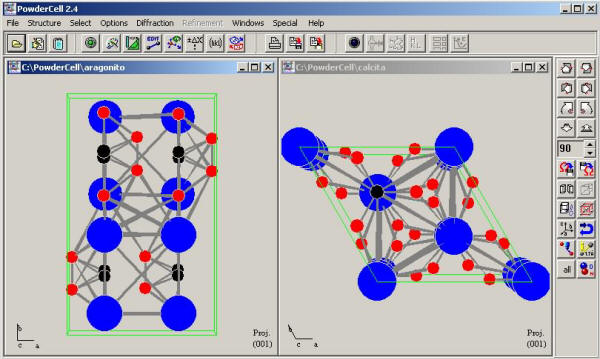
Ya podemos simular los difractogramas de rayos X de las dos fases (recuerda que es necesario tener abierto el dibujo de la estructura para poder generar su difractograma). Simplemente haremos clic en el icono 11 o ejecutaremos el comando {Diffraction -> Diffraction ON}. Se activa la ventana que nos muestra los dos difractogramas simultáneamente, el de la calcita en color rojo y el del aragonito en azul. En este momento estamos en disposición de poder comparar los dos difractogramas, para lo cual maximizamos la ventana.
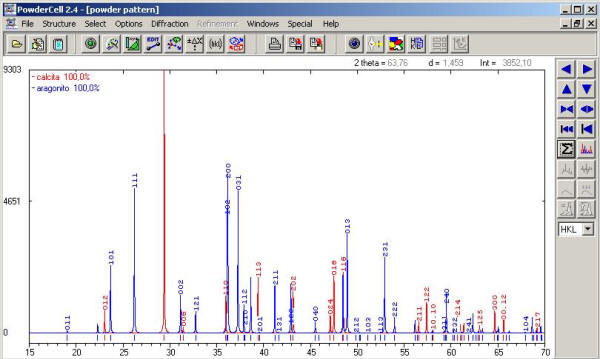
[Arriba]
3.- ¿Qué relación existe entre ambos difractogramas?
La posición de los máximos de difracción correspondientes a cada uno de los minerales es diferente. Para realizar un estudio más exhaustivo, consultemos la tabla en la que se muestran los parámetros de los máximos de difracción de cada uno de los dos minerales: pinchamos en el icono 14 ó ejecutamos {Diffraction –> HKL - List}. En el menú desplegable podremos escoger entre la lista de los máximos de difracción de la calcita o del aragonito

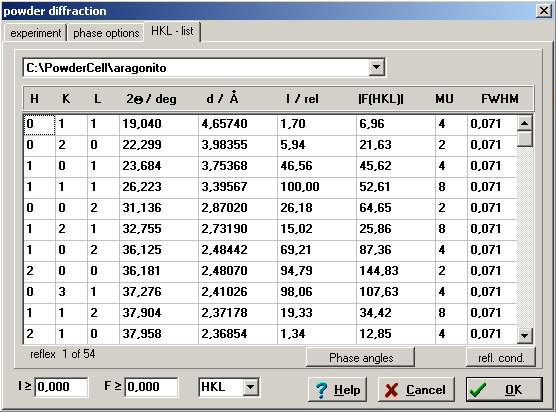
En efecto, los máximos de difracción de las fases son diferentes: sus posiciones (ángulo 2q/deg), sus índices de Miller (HKL), sus intensidades relativas (I/rel), etc. Fijémonos, por ejemplo, en el máximo de difracción más intenso presente en el difractograma de cada mineral:
|
Mineral |
Intensidad % |
Índice de Miller (hkl) |
Posición 2q(º) |
Espaciado reticular d(Å) |
| Calcita | 100 | (1 0 4) | 29.399 | 3.03571 |
| Aragonito | 100 | (1 1 1) | 26.223 | 3.39567 |
Podemos concluir que dos minerales con estructuras cristalinas diferentes generan diagramas de difracción diferentes. La calcita y aragonito, aunque tengan la misma composición química, CaCO3, poseen difractogramas distintos, por lo que son minerales polimorfos.
[Arriba]
4.- ¿Qué difractograma generará una mezcla de calcita y aragonito?
En el caso de que los minerales estudiados estuvieran presentes en una muestra policristalina ¿Cual sería el difractograma que obtendríamos? Este es el caso de una mezcla de fases. En el difractograma resultante de un experimento de difracción de rayos X coexistirían los máximos correspondientes a ambos minerales, pero no podríamos distinguir entre los correspondientes a uno o a otro mineral.
Podemos simular esta situación pinchando en el icono 27 (suma de difractogramas) y posteriormente en el que se encuentra a su derecha, con número 28 (elimina los difractogramas individuales de la calcita y del aragonito). El Difractograma resultante corresponderá a una muestra formada por una mezcla a partes iguales de calcita y aragonito. Compara este difractograma de la mezcla con el anteriormente simulado y verás que son equivalentes.
Difractogramas de la calcita y del aragonito superpuestos

Difractograma de una mezcla a partes iguales de calcita y aragonito.

Observa como en la parte superior derecha de este último difractograma PowderCell nos indica que tanto la calcita como el aragonito están presentes en un 100%. Esto quiere decir que el difractograma suma corresponde a un 200%, lo que no tiene mucho sentido. Para corregir esta situación, accederemos a la ventana que controla cada una de las fases de la mezcla pinchando en el icono 13 o en {Diffraction -> Phase options}. Entre otras cosas, podemos controlar el parámetro denominado factor de escala, que es proporcional a la cantidad de cada mineral presente en la hipotética muestra que difracta.
Sustituiremos el valor del factor de escala de 1.0 (es decir 100%) presente en scaling factor, por el de 0.5 (50%), tanto para la calcita como para el aragonito (el menú desplegable te permite pasar de un mineral a otro). Tras realizar esta operación y pulsar en OK observarás como se ha corregido este problema del 200%.

Este método permite simular los difractogramas de mezclas de fases con diferentes proporciones. Para concluir este apartado, incluimos dos difractogramas correspondientes a mezclas de calcita y de aragonito con diferentes proporciones.
Difractograma de una mezcla de 80% de calcita y 20% de aragonito.

Difractograma de una mezcla de 20% de calcita y 80% de aragonito.
