Ejemplos guiados

1. ¿Qué datos necesitamos para generar un difractograma?
2. ¿Cómo generar el difractograma de rayos X?
3. ¿Qué se puede hacer para analizar el difractograma?

[Ejemplos guiados][Página principal]

1.- ¿Qué datos necesitamos para generar un difractograma?

En primer lugar debemos realizar la búsqueda de los datos cristalográficos de este mineral. Para ello nos ayudaremos de la base de datos de estructuras de minerales AMCSD. Pasa saber como acceder a ella, visita la sección de recursos. Tras conectarnos a Internet y acceder a la base de datos, realizaremos la búsqueda utilizando como criterio el nombre del mineral en inglés: zircon.

La búsqueda da como resultado un total de 21 entradas, correspondientes a los modelos estructurales publicados en la revista American Mineralogist. Cada uno de ellos (en ocasiones un conjunto de ellos) es el resultado de un trabajo de investigación diferente sobre el mismo mineral: el circón. El modelo estructural a elegir depende de lo que nos propongamos estudiar. En nuestro caso, deseamos simular el diagrama de difracción, por lo que cualquiera de estos modelos estructurales nos servirá. La entrada de la base de datos elegida es la primera de éllas, que se muestra a continuación:

Para guardar esta información en nuestro ordenador, la forma más cómoda es: {Clic derecho sobre el nombre del mineral -> Guardar destino como -> Teclea el nuevo nombre de fichero (en este caso circón.amc y selecciona el directorio donde quieres guardarlo}. Obtendrás un fichero con la misma información y el mismo formato que la obtenida en la pantalla de tu ordenador. El resultado es un fichero con el siguiente contenido:

La información cristalográfica que hay que suministrar a PowderCell para representar la estructura cristalina y simular el diagrama de difracción esta marcado en negrita. Es la siguiente:

1. Parámetros de celda elemental (medido en Åmstrongs, Å): 6.607 6.607 5.982 90 90 90.
2. Grupo espacial de simetría: I4₁/amd. (Visita la tabla de grupos espaciales para conocer cual es su número)
3. Coordenadas (x, y, z) de los átomos de la unidad asimétrica:
   1. Zr     0.0    0.75    0.125
   2. Si     0.0    0.75    0.625
   3. O      0.0    0.0661  0.1953
4. Factores de ocupación de los átomos en su posición: el modelo estructural del circón que estamos utilizando no especifica factores de ocupación, por lo que se asume que su valor es de 1.0 (100%).

[Arriba]

2.- ¿Cómo podemos generar el difractograma de rayos X?

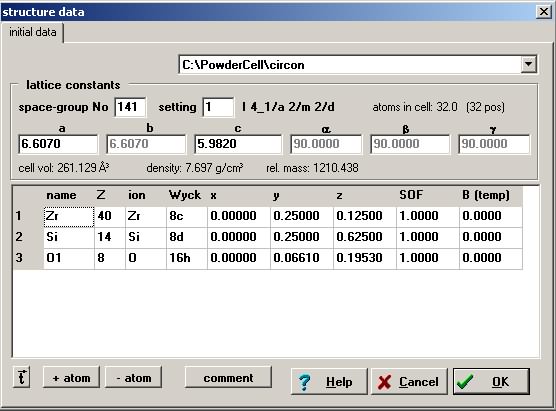
Una vez de estar en disposición de los datos cristalográficos del circón, debemos ejecutar el programa PowderCell para introducir los datos cristalográficos. Si no has instalado el programa en tu ordenador, visita la sección de recursos dedicada al programa PowderCell para saber como realizar la instalación.

En la ventana principal, ejecutamos {File -> New} y tecleamos los datos requeridos:

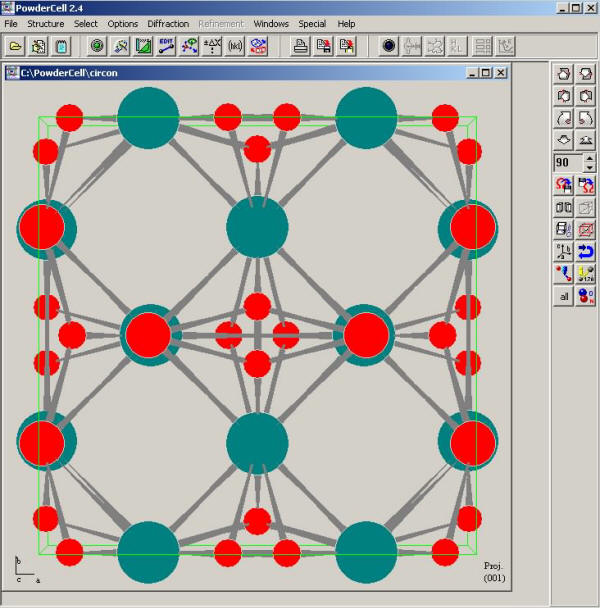
Tras introducidos los datos y haber pinchado en OK, se generará una representación gráfica de la estructura cristalina del circón.

Para evitar perder la información, generamos el fichero circon.cel en el directorio C:\PowderCell mediante el comando {File -> Save -> circon}. Si volvemos a visualizar los datos que acabamos de guardar en el fichero - mediante la opción {Estructure -> Edit initial data} o pinchando en el icono 2 - observamos que las coordenadas atómicas han sufrido variaciones. Esto se debe a que el programa introduce translaciones en las mismas. Además, PowderCell ha incluido datos que anteriormente no habíamos tecleado (Wyck, SOF, B(temp)).

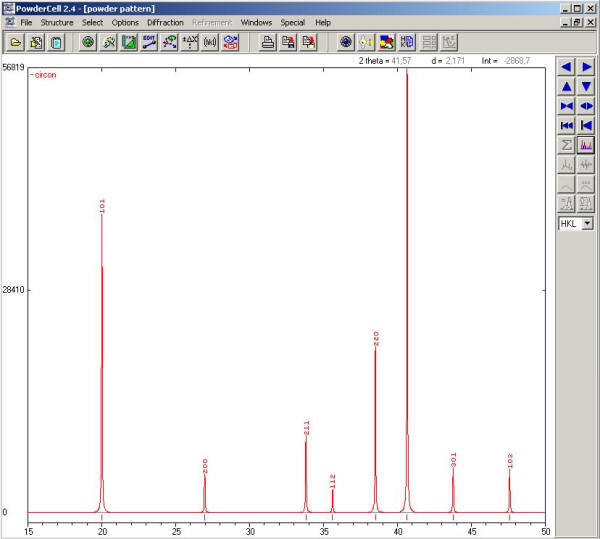
Una vez generada la representación gráfica de la estructura cristalina ya podemos simular el difractograma de rayos X del circón. Simplemente pinchando en el icono 11 se activará la ventana que nos muestra el difractograma. La siguiente figura es el resultado de maximizar la ventana que contiene la simulación del difractograma.

[Arriba]

3.- ¿Qué se puede hacer para analizar el difractograma?

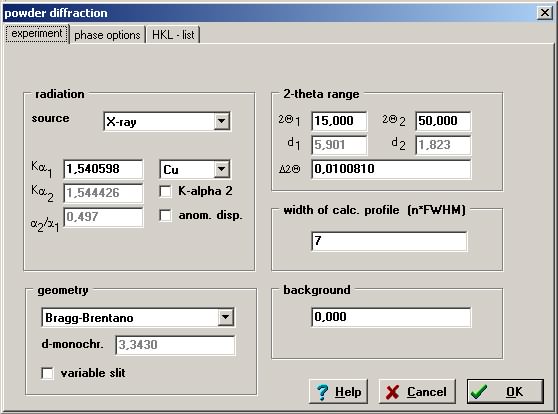
En primer lugar, prueba a pinchar y arrastrar el ratón sobre el difractograma. Verás que puedes ampliar la zona que desees. Además, los controles que se encuentran a la barra vertical de la derecha de la ventana (iconos 26) te permitirán moverte por el difractograma como desees. De especial utilidad es el menú desplegable que se encuentra justo debajo (icono 29), ya que con el puedes controlar la información contenida en la etiqueta que aparece encima de cada máximo de difracción.

Podemos obtener información sobre las variables utilizadas en la simulación del experimento de difracción haciendo clic sobre el icono 12 o ejecutando {Diffraction -> Experiment}. Se abrirá una nueva ventana en la cual, entre otros, aparecen los siguientes campos:

• Tipo de radiación utilizada (radiation):
  • Fuente de radiación: podemos seleccionar rayos X o neutrones.
  • Longitud de onda de la radiación: para el caso de los rayos X (tubos de rayos X con anticátodo de Cu, Mo, Fe...) o de los neutrones.
  • Radiación de rayos X monocromática o con doblete (Ka₁/Ka₂) y su relación de intensidades.
• Geometría del experimento difracción (geometry).
• Intervalo angular en 2q que se debe simular (2-theta range).
• Intensidad del fondo continuo del difractograma (background).

Es en esta ventada donde podemos estudiar cómo influye cada uno de estos parámetros en el difractograma, variando sus valores y repitiendo la simulación tantas veces como deseemos.

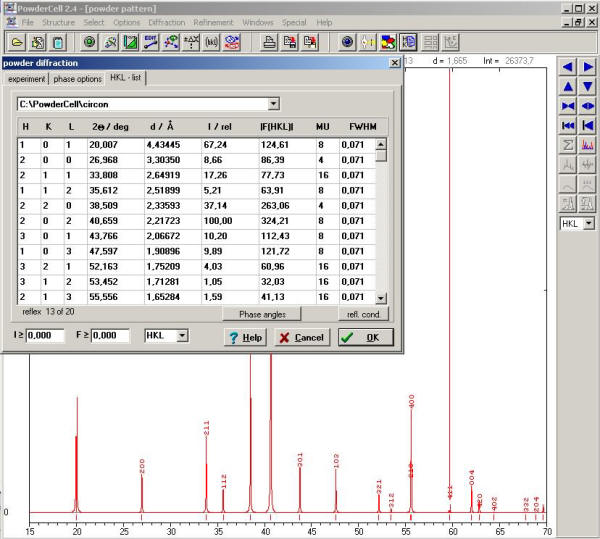
En esta misma ventana, seleccionando la pestaña HKL-list (o haciendo clic en el icono 14) obtendremos una tabla con los siguientes parámetros de los máximos de difracción presentes en el difractograma simulado:

• Índices de Miller (HKL).
• Ángulo de Bragg medido en grados (2/deg). Corresponde al eje horizontal del difractograma.
• Espaciado reticular medido en Å (d/Å): calculado mediante la Ley de Bragg.
• Intensidad relativa (I/rel): calculada en % con respecto al máximo más intenso del difractograma.
• Módulo del Factor de estructura (|F(hkl)|) asociado al máximo de difracción de índices de Miller (hkl).
• Multiplicidad del máximo (MU): calculado considerando el número de familias de planos reticulares que poséen el mismo espaciado reticular y que contribuyen a la intensidad de ese máximo.
• Anchura a media altura (FWHM) de cada máximo de difracción.

Pincha con el ratón sobre un máximo de difracción de la lista y aparecerá una línea vertical en el difractograma para indicarte donde se sitúa el máximo.