Ejemplos guiados

En esta sección encontrarás:
  1. ¿De qué información disponemos?
  2. Asignación de índices de Miller a los máximos del difractograma
  3. Identificación de la muestra problema

[Ejemplos guiados][Página principal]

Ejemplo A: muestra JS59

1.- ¿De qué información disponemos?

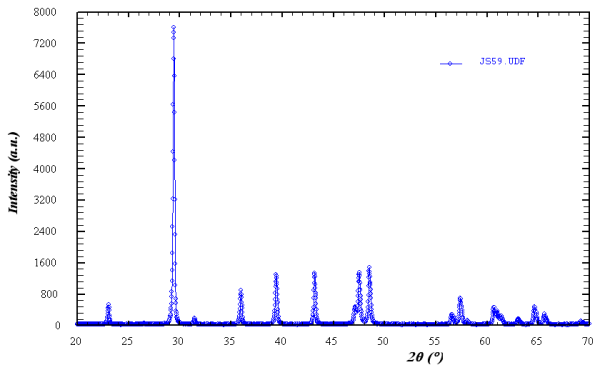
En el diagrama de difracción de la muestra JS59 hay un total de 18 máximos, situados en las siguientes posiciones:

Máximo

Posición (2q)

Posición (d)

Intensidad (cuentas)

Intensidad (%)

Fondo continuo (cuentas)

1

23.06019

3.8535

528.49902

7.0

27.19396

2

29.41685

3.0337

7599.86572

100.0

71.46364

3

31.46288

2.8409

188.00920

2.5

24.02336

4

35.97953

2.4940

904.67743

11.9

28.92200

5

39.41782

2.2840

1280.34888

16.8

39.66861

6

43.16999

2.0937

1326.09412

17.4

36.39025

7

47.12910

1.9267

469.06433

6.2

84.00769

8

47.52411

1.9116

1344.17700

17.7

98.95063

9

48.50658

1.8751

1456.69763

19.2

86.19741

10

56.56706

1.6256

275.69003

3.6

56.15483

11

57.39853

1.6040

672.30896

8.8

54.04197

12

58.08961

1.5865

122.54144

1.6

41.92734

13

60.67128

1.5251

450.00696

5.9

44.96465

14

60.97923

1.5181

371.56430

4.9

49.09768

15

63.06043

1.4729

174.21404

2.3

20.29751

16

64.66052

1.4403

479.85178

6.3

49.94180

17

65.62788

1.4214

281.09055

3.7

44.49326

18

69.18520

1.3567

114.13897

1.5

26.06868
 

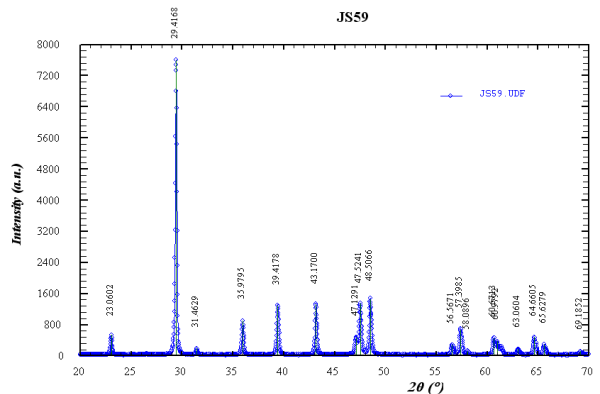
Como ya vimos en la sección dedicada al programa DICVOL91, la posición de los máximos de difracción se suele dar en espaciados reticulares, d, medidos en Åmstrongs, Å (1Å = 10-10m). Esta transformación se realiza mediante la Ley de Bragg, l=2dsen(q). La longitud de onda de los rayos X utilizados es la de un tubo de rayos X con anticátodo de cobre, CulKa1=1.5406Å.

[Arriba]

2.- Asignación de índices de Miller a los máximos de difractograma

La asignación de índices de Miller y la deducción de los parámetros de celda de la fase desconocida la realizaremos con el programa DICVOL91. Para ello debe generarse el fichero de entrada correspondiente. En este caso, utilizaremos las condiciones estándar de búsqueda de posibles soluciones, explorando en primera instancia los sistemas cristalinos de más alta simetría (excluyendo el sistema monoclínico y triclínico).

El fichero de entrada al programa DICVOL91, de nombre JS59.dic, contiene la información necesaria para la búsqueda de posibles celdas elementales. Ejecuta el programa DICVOL91 con este fichero para familiarizarte con el funcionamiento del programa y con los ficheros de salida {para guardar JS59.dic en tu ordenador: Clic derecho -> Guardar destino como -> Selecciona un directorio para guardarlo}

 JS59
  18   2   1   1   1   1   0   0
   20.0   20.0   20.0    0.0 1500.0   90.0  125.
  1.54060    0.000    0.000    0.
    0.000    0.000   1
      23.06019
      29.41685
      31.46288
      35.97953
      39.41782
      43.16999
      47.12910
      47.52411
      48.50658
      56.56706
      57.39853
      58.08961
      60.67128
      60.97923
      63.06043
      64.66052
      65.62788
      69.18520

Tras ejecutar el programa DICVOL91 la búsqueda de índices de Miller da como resultado dos posible celdas elementales, con figuras de mérito elevadas. En el fichero de salida JS59.ucp encontrarás la siguiente información

 DICVOL CONDENSED RESULTS:
   . input  file: JS59.dic
   . output file: JS59.ind
   . INSTRM:-99
 a(A)     b(A)    c(A)     alfa  beta  gama  symmetry  Volume(A3)  M(18)  M'(18)  F(18)
---------------------------------------------------------------------------------------
 4.9894  4.9894  17.0571  90.0  90.0  120.0   Hexag.    367.73     59.4   297.0   41.1
17.0568  4.9889   4.3215  90.0  90.0   90.0   Orthorh.  367.74     28.3   113.4   19.7
 

Ambas soluciones presentan el mismo volumen de celda, por lo que, en principio pueden considerarse dos geometrías distintas de la celda unidad de nuestro compuesto. Para realizar la elección de la mejor celda elemental deberemos prestar atención a criterios tales como:

  1. Sistema cristalino: debemos escoger el de mayor simetría

  2. Figuras de mérito M(n): En nuestro caso, M(18). Cuanto mayor sea el valor de la figura de mérito, más probable es que la solución sea la correcta. Nosotros obtenemos un valor de 59.4 para M(18).

Según estas consideraciones, la celda unidad hexagonal es la primera a tener en cuenta. La asignación de los índices de Miller utilizando esta celda elemental la podemos encontrar en el fichero de salida JS59.ind del programa DICVOL90 :

                     H E X A G O N A L    S Y S T E M

      DIRECT PARAMETERS :    A=  4.98936  C= 17.05713    VOLUME=   367.73
      STANDARD DEVIATIONS :      0.00034      0.00222

   H   K   L    DOBS     DCAL   DOBS-DCAL  QOBS  QCAL  2TH.OBS  2TH.CAL DIF.2TH.

   1   0   2  3.85376  3.85445 -0.00069 0.067330.06731  23.060  23.056  0.004
   1   0   4  3.03387  3.03513 -0.00126 0.108640.10855  29.417  29.404  0.012
   0   0   6  2.84109  2.84286 -0.00177 0.123890.12373  31.463  31.443  0.020
   1   1   0  2.49411  2.49468 -0.00057 0.160760.16068  35.980  35.971  0.008
   1   1   3  2.28412  2.28446 -0.00034 0.191670.19162  39.418  39.412  0.006
   2   0   2  2.09388  2.09431 -0.00042 0.228080.22799  43.170  43.161  0.009
   2   0   4  1.92680  1.92723 -0.00043 0.269360.26924  47.129  47.118  0.011
   1   0   8  1.91170  1.91203 -0.00033 0.273630.27353  47.524  47.515  0.009
   1   1   6  1.87525  1.87509  0.00016 0.284370.28442  48.507  48.511 -0.004
   2   1   1  1.62567  1.62572 -0.00005 0.378390.37836  56.567  56.565  0.002
   2   1   2  1.60408  1.60401  0.00007 0.388640.38867  57.399  57.401 -0.003
   1   0  10  1.58663  1.58657  0.00007 0.397230.39727  58.090  58.092 -0.003
   2   1   4  1.52515  1.52513  0.00002 0.429910.42992  60.671  60.672 -0.001
   2   0   8  1.51818  1.51756  0.00062 0.433860.43422  60.979  61.007 -0.028
   2   1   5  1.47299  1.47305 -0.00006 0.460890.46085  63.060  63.058  0.003
   3   0   0  1.44035  1.44031  0.00005 0.482020.48205  64.661  64.663 -0.002
   0   0  12  1.42145  1.42143  0.00002 0.494920.49494  65.628  65.629 -0.001
   2   1   7  1.35679  1.35663  0.00015 0.543220.54334  69.185  69.194 -0.009

          * NUMBER OF LINES
               .- INPUT DATA =  18
               .- CALCULATED =  58

          * MEAN ABSOLUTE DISCREPANCIES
                                              <Q> =0.7884E-04
                                 <DELTA(2-THETA)> =0.7552E-02
               MAX. ERROR ACCEPTED (DEG. 2-THETA) =0.4500E-01

          * FIGURES OF MERIT
                 1.- M( 18)  =   59.4                         (REF. 4)
                 2.- M'( 18) =  297.0                         (REF. 8)
                 3.- F( 18)  =   41.1(0.0076,  58)            (REF. 5)

[Arriba]

3.- Identificación de la muestra problema

Una vez seleccionada la celda más probable – junto con la asignación de los índices de Miller a cada máximo de difracción – podemos decir que disponemos de la huella dactilar completa de nuestro material problema.

Pasemos a continuación a comparar esta información con las huellas dactilares de los numerosos compuestos incluidas en la base de datos PDF (Powder Diffraction File). Para ello, debemos acceder a la ventana de búsquedas del programa que gestiona dicha base de datos, PCPDFWIN:

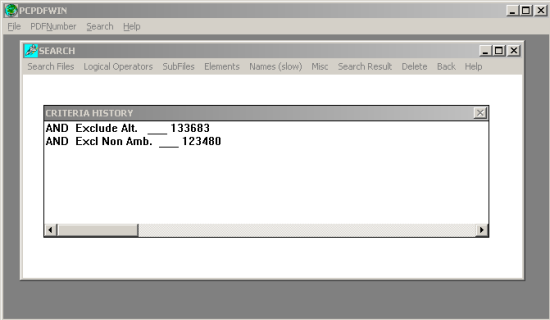
 De las 123480 fichas de compuestos disponible, debemos seleccionar aquellas que cumplan las características cristalográficas de nuestro compuesto problema. Las diferentes posibilidades de búsqueda se encuentran en los diversos menús. Con la información de que disponemos, el menú más indicado para nosotros es Misc (misceláneos), con las siguientes criterios de selección:

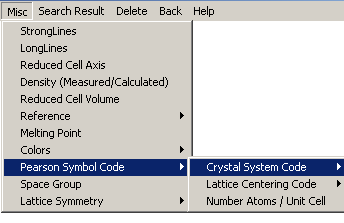
  En este caso, utilizaremos:

  • La posición de los tres máximos de difracción más intensos (Strong Line): máximos 2 (3.0337Å, 100%), 9 (1.8751Å, 19.2%) y 8 (1.9116Å, 17.7%).

  • La posición de los tres máximos de difracción con mayores espaciados reticulares (Long Line): máximos 1 (3.8535Å), 2 (3.0337Å) y 3 (2.8409Å).

  • Las dimensiones de los parámetros de celda (Reduced Cell Axis): comprendidos entre 4.5 y 17.5Å.

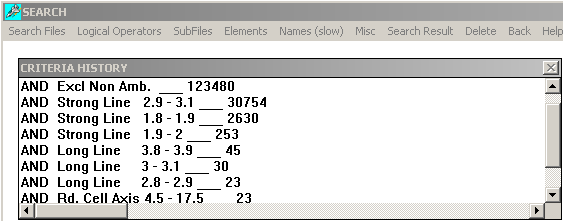
 Como vemos, el último criterio no reduce el número de posibles compuestos candidatos, 23. Podríamos continuar introduciendo restricciones a la búsqueda, pero echemos un vistazo a la lista de candidatos (Search Result):

Ficha

Sustancia

Fórmula

Max. intensos

Sist.

89-1305

Magnesium calcite - synthetic, Mag-

(Mg0.06Ca0.94)-

3.02 1.86 1.90

R

89-1304

Magnesium calcite, syn, Magnesium -

(Mg0.03Ca0.97)-

3.03 1.87 1.91

R

89-0311

Sodium Nitrate

Na(NO3)

3.04 2.31 1.90

R

89-0310

Sodium Nitrate

Na(NO3)

3.04 2.31 1.90

R

88-1807

Calcite, Calcium Carbonate

Ca(CO3)

3.04 1.88 1.91

R

86-2335

Calcite magnesian, Magnesium Calci-

(Mg.064Ca.936 -

3.02 1.87 1.90

R

86-0174

Calcite, syn, Calcium Carbonate

Ca(CO3)

3.04 1.88 1.91

R

85-1467

Nitratine, syn, Sodium Nitrate

Na(NO3)

3.04 2.31 1.90

R

85-1108

Calcium Carbonate

CaCO3

3.03 1.91 1.87

R

83-0578

Calcite, Calcium Carbonate

Ca(CO3)

3.03 1.87 1.91

R

83-0577

Calcite, Calcium Carbonate

Ca(CO3)

3.03 1.87 1.91

R

81-2027

Calcite, syn, Calcium Carbonate

Ca(CO3)

3.04 1.88 1.91

R

79-2056

Sodium Nitrate

NaNO3

3.04 2.31 1.90

R

76-2243

Nitratine, syn, Sodium Nitrate

NaNO3

3.04 2.31 1.90

R

72-1213

Nitratine, syn, Sodium Nitrate

NaNO3

3.04 2.31 1.90

R

72-0025

Nitratine, syn, Sodium Nitrate

NaNO3

3.04 2.31 1.90

R

71-2010

Sodium Nitrate

NaNO3

3.04 2.31 1.90

R

70-1518

Nitratine, syn, Sodium Nitrate

NaNO3

3.04 2.31 1.90

R

47-1743

Calcite, Calcium Carbonate

CaCO3

3.04 1.88 1.91

R

36-1474

Nitratine, Sodium Nitrate

NaNO3

3.04 2.31 1.90

R

32-0160

Calcium Copper Fluoride

CaCuF4

3.07 1.87 1.91

T

04-0637

Calcite, Calcium Carbonate

CaCO3

3.04 1.91 1.88

R

04-0636

Calcite, Calcium Carbonate

CaCO3

3.04 1.91 1.88

R

Únicamente son tres los compuestos distintos que aparecen en la lista: calcita, nitratina y fluoruro de calcio y sodio. La comparación de las diferentes fichas con los datos de que disponemos (máximos de difracción y parámetros de celda), permite concluir que nuestro material problema es calcita, Ca(CO3). Examina la ficha 88-1807 y compara la información que contiene con la de nuestro material, para comprobar que la identificación es correcta.

Posición de los máximos de difracción expresados en grados 2q

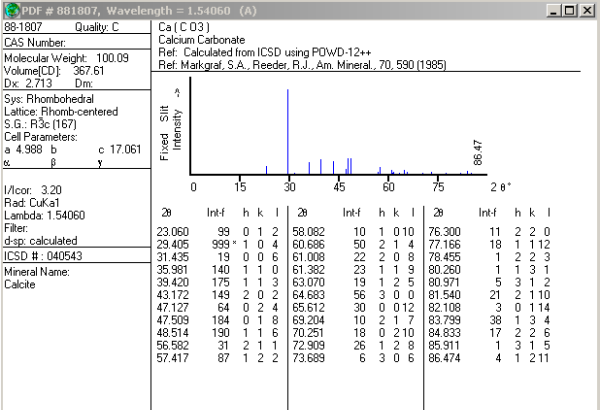
Posición de los máximos de difracción expresados en espaciados reticulares, d(Å)

 

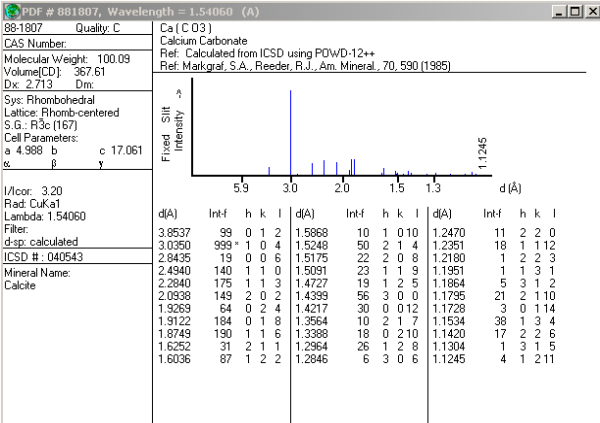
[Arriba][Siguiente: Ejemplo B][Ejemplos guiados][Página principal]

Última actualización: 21/12/2004