1.- ¿De qué información disponemos?
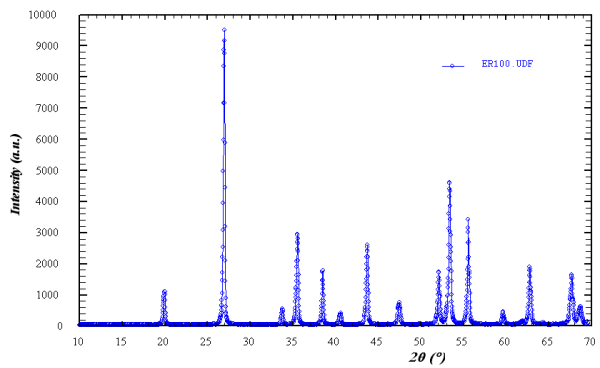
En el diagrama de difracción de la muestra UR100 hay un total de 16 máximos, situados en las siguientes posiciones:
|
Máximo |
Posición (2q) |
Posición (d) |
Intensidad (cuentas) |
Intensidad (%) |
Fondo continuo (cuentas) |
|
1 |
19.97433 |
4.4413 |
1088.36230 |
11.5 |
39.29919 |
|
2 |
26.95226 |
3.3052 |
9472.86816 |
100.0 |
87.74263 |
|
3 |
33.77390 |
2.6516 |
558.70642 |
5.9 |
52.03078 |
|
4 |
35.54523 |
2.5234 |
2932.26831 |
31.0 |
61.54189 |
|
5 |
38.49244 |
2.3367 |
1768.94238 |
18.7 |
42.65920 |
|
6 |
40.58926 |
2.2207 |
411.74280 |
4.3 |
50.57919 |
|
7 |
43.71727 |
2.0688 |
2591.16431 |
27.4 |
82.54862 |
|
8 |
47.47023 |
1.9136 |
767.99030 |
8.1 |
45.70176 |
|
9 |
52.10496 |
1.7538 |
1729.64111 |
18.3 |
115.48173 |
|
10 |
53.37479 |
1.7150 |
4631.11719 |
48.9 |
152.25555 |
|
11 |
55.54844 |
1.6529 |
3418.10840 |
36.1 |
83.83794 |
|
12 |
59.63324 |
1.5491 |
462.03976 |
4.9 |
62.24660 |
|
13 |
62.76522 |
1.4791 |
1846.06494 |
19.5 |
105.44768 |
|
14 |
64.28952 |
1.4477 |
112.35458 |
1.2 |
49.34914 |
|
15 |
67.67625 |
1.3832 |
1646.21741 |
17.4 |
175.81261 |
|
16 |
68.69260 |
1.3652 |
614.76776 |
6.5 |
145.18173 |
[Arriba]
2.- Asignación de índices de Miller a los máximos de difractograma
La asignación de índices de Miller y la deducción de los parámetros de celda de la fase la realizaremos en este caso con el programa TREOR90. Para ello debe generarse el fichero de entrada correspondiente, que llamaremos ER100.inp. En este caso, utilizaremos las condiciones estándar de búsqueda de posibles soluciones, explorando los sistemas cristalinos de más alta simetría (excluyendo el sistema monoclínico [MONO=0] y triclínico).
Fichero de entrada al programa TREOR90 ER100.inp {para guardarlo en tu ordenador: Clic derecho -> Guardar destino como -> Selecciona un directorio para guardarlo}
ER100
19.97433
26.95227
33.77390
35.54523
38.49244
40.58926
43.71727
47.47023
52.10496
53.37479
55.54844
59.63324
62.76523
64.28952
67.67625
68.69260
CHOICE=3,
WAVE= 1.54060,
MONO=0.00,
VOL= 1500.,
CEM= 20.,
MERIT= 10.,
END*
La búsqueda de índices de Miller da como mejor resultado una posible celda elemental, con figuras de mérito elevadas. Sus parámetros de celda se incluyen en el fichero de salida ER100.cry del programa TREOR90:
Treor
solution (Automatic generated CRY file)
TETR
P4/MMM
6.6133 6.6133 5.9966 90.0000 90.0000 90.0000
Podemos encontrar la asignación de los índices de Miller a los máximos de difracción utilizando esta celda elemental, junto con la figura de mérito correspondiente, M(16), en el fichero de salida ER100.cnd del programa TREOR90 :
VERSION JANUARY 1990
ER100
19.974331
26.952271
33.773899
35.545231
38.492439
40.589260
43.717270
47.470230
52.104961
53.374790
55.548439
59.633240
62.765228
64.289520
67.676247
68.692596
LINE NUMBER= 6 SHOULD NOT BE INCLUDED IN THE TREOR
BASE LINE SETS. SINE SQUARE THETA FOR THIS LINE = 4
TIMES SINE SQUARE THETA FOR LINE NUMBER = 1
LINE NUMBER= 6 WILL BE SKIPPED IN THE TRIAL PHASE.
STOP LIMITS
FIGURE OF MERIT REQUIRED= 10
MAX NUMBER OF UNINDEXED LINES IN FIGURE OF MERIT TEST= 1
THE 7 FIRST LINES ADJUSTED BY THEIR HIGHER ORDERS
CUBIC,TETRAGONAL,HEXAGONAL AND ORTHORHOMBIC SYMMETRY
MAX CELL EDGE= 20.0 MAX CELL VOLUME= 1500.0
D1= 0.000200 SSQTL= 0.050000 D2= 0.000400 WAVE= 1.540600
NUMBER OF TEST LINES= 15 IQ REQUIRED= 12
** CUBIC TEST ********************* MAX. VOLUME= 1500.
SELECTED BASE LINES (1) (2)
BASE LINE ONE.(HKL)-MAX= 4 4 4 MAX H+K+L= 6
** TETRAGONAL TEST **************** MAX. VOLUME= 1500.
SELECTED BASE LINES (1,2) (1,3) (2,3)
BASE LINE ONE.(HKL)-MAX= 4 4 4 MAX H+K+L= 4
BASE LINE TWO.(HKL)-MAX= 4 4 4 MAX H+K+L= 4
THIS MAY BE THE SOLUTION !!!
THE REFINEMENT OF THE CELL WILL NOW BE REPEATED
THREE CYCLES MORE. --- GOOD LUCK !
CYCLE RESULTS
0.013567 0.016501 0.000000 0.000000 0.000000 0.000000
0.013567 0.016501 0.000000 0.000000 0.000000 0.000000
0.013567 0.016501 0.000000 0.000000 0.000000 0.000000
NUMBER OF SINGLE INDEXED LINES = 16
TOTAL NUMBER OF LINES = 16
A = 6.613338 0.000442 A ALFA = 90.000000 0.000000 DEG
B = 6.613338 0.000442 A BETA = 90.000000 0.000000 DEG
C = 5.996556 0.000720 A GAMMA = 90.000000 0.000000 DEG
UNIT CELL VOLUME = 262.27 A**3
H K L SST-OBS SST-CALC DELTA 2TH-OBS 2TH-CALC D-OBS FREE
PARAM.
1
0 1 0.030076 0.030068 0.000008 19.974 19.971 4.4417
2 0 0 0.054286 0.054267 0.000019 26.947 26.942
3.3061
2 1 1 0.084381 0.084335 0.000046 33.774 33.764
2.6518
1 1 2 0.093172 0.093139 0.000033 35.545 35.539
2.5236
2 2 0 0.108655 0.108535 0.000120 38.492 38.470
2.3369
2 0 2 0.120303 0.120272 0.000031 40.589 40.584
2.2209
3 0 1 0.138621 0.138603 0.000018 43.717 43.714
2.0689
1 0 3 0.162013 0.162078 -0.000064 47.470 47.480
1.9137
3 2 1 0.192892 0.192870 0.000022 52.105 52.102
1.7539
3 1 2 0.201711 0.201673 0.000038 53.375 53.369
1.7151
4 0 0 0.217145 0.217069 0.000076 55.548 55.538
1.6530
4 1 1 0.247233 0.247137 0.000096 59.633 59.620
1.5492
4 2 0 0.271181 0.271337 -0.000155 62.765 62.785
1.4792
4 0 2 0.283088 0.283074 0.000014 64.290 64.288
1.4478
3 3 2 0.310080 0.310208 -0.000128 67.676 67.692
1.3833
2 0 4 0.318314 0.318287 0.000027 68.693 68.689
1.3653
NUMBER OF OBS. LINES = 16
NUMBER OF CALC.
LINES
= 16
M( 16)= 58 AV.EPS.= 0.0000560
F 16 = 39.(0.008554, 49)
M CF. J.APPL.CRYST. 1(1968)108
F
CF. J.APPL.CRYST. 12(1979)60
0
LINES ARE UNINDEXED
M-TEST= 58 UNINDEXED IN THE TEST= 0
ANY COMMON FACTOR IN THE QUADRATIC FORMS ? ?
CHECK
CONVERGENCE IN THE REFINEMENT
(EV.
USE PROGRAM PIRUM OR PURUM)
END
OF INDEXING CALCULATIONS
SET KS=0 AND THS=0 TO CHECK THE SOLUTION....
AND RUN TREOR ONCE MORE.
IF YOU WANT TO LOOK FOR A BETTER SOLUTION YOU
MAY TRY TO INCREASE THE PARAMETER MERIT ABOVE 58
....OR PERHAPS THIS WAS THE BEST SOLUTION...
[Arriba]
3.- Identificación de la muestra problema
Una vez obtenida la celda elemental más probable – junto con la asignación de los índices de Miller a cada máximo de difracción – podemos decir que disponemos de la huella dactilar completa de nuestro material.
Pasemos a continuación a comparar esta información con las huellas dactilares de los numerosos compuestos incluidas en la base de datos PDF (Powder Diffraction File). Para ello, debemos acceder a la ventana de búsquedas del programa que gestiona dicha base de datos, PCPDFWIN.
Los criterios de búsqueda que utilizaremos en este caso serán:
-
El sistema cristalino: tetragonal
-
La posición de los tres máximos con mayores espaciados reticulares (Long Line): máximos 1 (4.4413Å), 2 (3.3052Å) y 3 (2.6516Å).
-
La posición del máximo de difracción más intenso (Strong Line): máximo 2 (3.3052Å, 100%).
-
Las dimensiones de los parámetros de celda (Reduced Cell Axis): comprendidos entre 5.5 y 7.0Å.
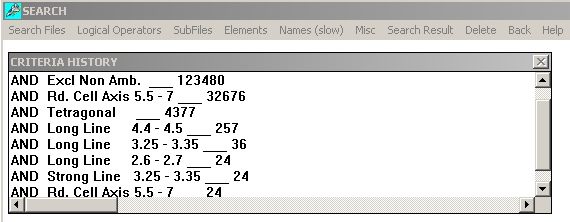
Como vemos, los dos último criterios no reducen el número de posibles compuestos candidatos, 24. Podríamos continuar introduciendo restricciones a la búsqueda, pero echemos un vistazo a la lista de candidatos (Search Result):
|
Ficha |
Sustancia |
Fórmula |
Max. intensos |
Sist. |
|
89-0881 |
Zirconium Silicate Hydroxide Fluor |
Zr(SiO4)0.206- |
4.42 3.32 1.71 |
T |
|
89-0880 |
Zirconium Silicate Hydroxide Fluor |
Zr(SiO4)0.305- |
4.42 3.32 1.71 |
T |
|
88-0278 |
Antimony Vanadium Oxide |
(SbV)O4 |
3.26 2.56 1.71 |
T |
|
83-1374 |
Zircon, Zirconium Silicate |
ZrSiO4 |
3.30 2.52 1.71 |
T |
|
81-0589 |
Zircon, Zirconium Silicate |
Zr(SiO4) |
3.30 2.53 1.71 |
T |
|
81-0588 |
Zircon, Zirconium Silicate |
Zr(SiO4) |
3.31 2.53 4.44 |
T |
|
81-0140 |
Zirconium Hafnium Vanadium Oxide S |
(Zr0.988Hf0.012- |
3.30 2.52 1.71 |
T |
|
81-0139 |
Zirconium Hafnium Silicate |
(Zr0.988Hf0.012- |
3.30 2.52 1.71 |
T |
|
80-1809 |
Zircon, syn, Zirconium Silicate |
Zr(SiO4) |
3.30 2.52 1.71 |
T |
|
80-1808 |
Zircon, syn, Zirconium Silicate |
Zr(SiO4) |
3.30 2.52 1.71 |
T |
|
80-1807 |
Zircon, syn, Zirconium Silicate |
Zr(SiO4) |
3.31 2.53 1.72 |
T |
|
77-1759 |
Hafnium Silicate |
HfSiO4 |
3.29 4.43 2.52 |
T |
|
76-0865 |
Zircon, Zirconium Silicate |
ZrSiO4 |
3.30 2.52 1.71 |
T |
|
75-1628 |
Hafnon, syn, Hafnium Silicate |
HfSiO4 |
3.29 4.42 2.51 |
T |
|
75-1590 |
Zircon, Zirconium Silicate |
ZrSiO4 |
3.29 2.50 4.41 |
T |
|
72-0402 |
Zircon, Zirconium Silicate |
ZrSiO4 |
3.30 2.52 4.43 |
T |
|
71-0991 |
Zircon, Zirconium Silicate |
ZrSiO4 |
3.31 2.52 1.71 |
T |
|
20-0467 |
Hafnon, syn, Hafnium Silicate |
HfSiO4 |
3.29 2.51 4.43 |
T |
|
06-0266 |
Zircon, Zirconium Silicate |
ZrSiO4 |
3.30 4.43 2.52 |
T |
|
03-0460 |
Zircon, Zirconium Silicate |
ZrSiO4 |
3.29 1.71 2.52 |
T |
|
03-0459 |
Zircon, Zirconium Silicate |
ZrSiO4 |
3.29 1.71 2.52 |
T |
|
03-0457 |
Zircon, Zirconium Silicate |
ZrSiO4 |
3.30 1.71 2.52 |
T |
|
03-0456 |
Zircon, Zirconium Silicate |
ZrSiO4 |
3.30 1.71 2.52 |
T |
|
01-0679 |
Zircon, Zirconium Silicate Oxide |
ZrSiO4 |
3.29 2.51 1.71 |
T |
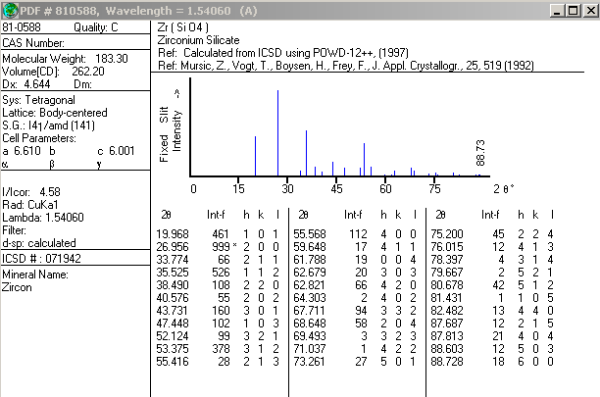
Analizando los resultados se deduce que varias fichas corresponden al mismo compuesto, por lo que el número de posibilidades se reduce considerablemente. Comparando estas fichas con los datos de nuestro compuesto problema (máximos de difracción y parámetros de celda), se concluye que se trata de circón, Zr(SiO4), Ficha PDF Nº 81-0588.
Posición de los máximos de difracción expresados en grados 2q
![]()
Posición de los máximos de difracción expresados en espaciados reticulares, d(Å)