DESKRIBAPENA

Doppler-efektua

Doppler-efektua soinu uhinetan hau da: jasotako maiztasuna eta igorritakoa ez dira berdinak, eta maiztasunaren aldaketa soinu igorleak edota behatzaileak medioarekiko duten higiduraren menpekoa da. Frekuentzia handitzen da igorlea eta hartzailea hurbiltzen ari direnean eta gutxitu egiten da urruntzen ari direnean.

Zurgapena

Soinu-uhin bat horma zurrun batera iristen denean (horma ideala) guztiz islatzen da, horma ez delako mugitzen eta ez duelako uhinaren energiarik zurgatzen. Horma errealak ordea, ez dira erabat zurrunak eta uhin erasotzaileen energiaren parte bat zurga dezakete.

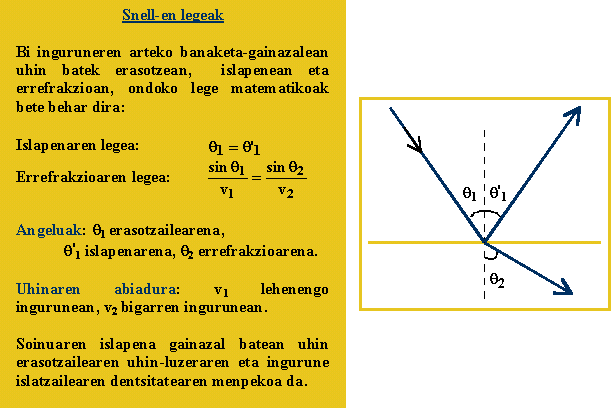
Islapena eta errefrakzioa. Transmisioa

Uhin bat muga batera iristen denean (muga da bi medio ezberdin banatzen dituen gainazala), uhinaren parte bat islatu egiten da, beste bat disipatu eta beste bat transmititu. Uhinen propagazio-abiadura, v, aldatu egiten da medio batetik bestera pasatzerakoan, baina w maiztasuna ez da aldatzen.

Uhin erasotzailea mugara iristean, angelu jakin batez erasotzen badu, uhin transmitituaren norabidea ez da jatorrizkoaren berdina, normaletik hurbilago edo urrunago baizik. Uhinaren desbideraketa honi errefrakzio deritzo.

Difrakzioa

Uhinek oztopoak inguratu eta gainditu egin ditzakete eta irekigune txikietatik ere pasa daitezke: hauxe da Difrakzioa. Fenomeno hau orokorra da, hau da, uhin-mota guztietan gertatzen da baina nabarmenagoa da uhinaren uhin-luzera eta oztopo edo irekigunearen tamaina antzekoak direnean. Irekigune bat (edo oztopoa) handia bada uhin-luzerarekin konparatuta, difrakzioaren efektua oso apala da eta uhina ibilbide zuzenean propagatzen da, edo izpietan, partikula-sorta batek egiten duen antzera. Baina irekigunearen tamaina (edo oztopoarena) uhin-luzeraren antzekoa bada, difrakzioaren efektua nabarmena da eta uhina ez da soilik zuzenki propagatzen, dispertsatu ere egiten da irekigunea iturri puntual bat bailitzan.

Soinu entzungaiaren uhin-luzerak 3 cm eta 12 m bitartekoak dira eta normalean handiak izaten dira ohizko oztopo eta irekiguneekin konparatuta (adibidez ateak eta leihoak), horregatik soinua desbideratu egiten da eta oztopoak inguratzen ditu.

Erradiazioa

Iturburu bibratzaile baten energia airea bezalako medio batera igortzea ahalbidetzen duen prozesuari Erradiazioa deritzo.

Oihartzuna eta erreberberazioa

Soinu baten sentsazioa desagertu eta gero, berriro ere entzuten denean oihartzuna deritzo, eta gertatzen da, adibidez, soinua horma batean perpendikularki islatzen denean. Giza belarriak denboran bereiz ditzake iraunkortasun-denbora baino separatuagoak diren soinuak:  0.1 segundo, musika soinuetan eta 0.07 segundo soinu idorretan (hitzetan). Beraz belarriak soinu bat zuzenean jaso ondoren eta iraunkortasun-denbora baino geroago islatutako soinua jasotzen badu, oihartzunaren efektua nabarituko du. Oihartzuna nabaritzeko horma islatzailea soinu-iturritik 17 metrora egon behar da soinu musikaletarako, eta 11.34 metrora soinu idorretarako.

Erreberberazioa ordea, islatutako soinua uhin zuzena bukatu baino lehen iristen denean gertatzen da, hau da, soinuaren iraunkortasun-denbora baino lehenago. Fenomeno hau oso garrantzitsua da soinua entzun behar den aretoetan. Entzuleak ez du soilik uhin zuzena jasotzen, hormetako islapen ezberdinak ere bai. Efektu hau kontuz kontrolatuz, aretoetako baldintza akustikoak hobetu nahi izaten dira, adibidez antzokietan, hitzaldi edo kontzertu-aretoetan, eta orokorrean areto-mota askotan. Areto baten erreberberazioa deskribatzen duen magnitudea aretoaren erreberberazio-denbora da: soinu baten intentsitatea bere hasierako balioaren milioirena izatera jaisteko behar duen denbora.

ADIBIDE ETA SIMULAZIOAK

Doppler-efektua

Ondorengo simulazioan Doppler-efektua azter daiteke. Soinu-igorle batek etengabe emititzen du, baina irudian uhin-fronte kontsekutiboak soilik irudikatzen dira, hau da, periodo bakoitzean igorleak emititzen duen frontea zirkularki bere inguruan hedatuz, baina igorlea mugitzen ari dela. Laborategiko esperientzian ur-ontzi batean ere gauza bera beha daiteke.

Instrukzioak

Soinuaren abiadura medioan finkoa da eta unitatetzat hartu da: v_s = 1, eta uhinen periodoa ere unitatea da. Horregatik uhin-fronte kontsekutiboak periodo batean luzera-unitate bat desplazatuta daude, hau da, igorritako uhin-luzera ere unitatea da: l_e= 1.

1. Behatzailea geldi (v_o = 0)

Kasu sinpleenetik hasiko gara, behatzailea geldi dagoenean (simulazioan behatzaile bat igorlearen ezkerrean eta beste bat eskuman). Igorlearen abiaduraren arabera, kasu ezberdinak azalduko dira: 

1. Igorlearen abiadura kontrolean, idatz ezazu abiadura baina betiere soinuaren abiadurarekiko dela gogoratuz eta ondorengo kasuak kontutan hartuta:

2. Simulazioa hasteko, gelditzeko eta pausoka ikusteko Hasi, Geldi eta Pausu botoiak klikatu behar dira.

1. Igorlea geldi (v_e = 0)

Azter ezazu nolakoak diren uhin-fronte kontsekutiboak: zirkunferentziak, denak igorlean zentratuta eta uhin-luzera bateko distantziaz. Zirkunferentzia bakoitzaren erradioa handituz doa, igorri denetik pasatako denbora eta soinuaren abiaduraren arteko biderkadura delako.

Egiazta ezazu igorleak eta behatzaileak neurtutako uhin-luzera (uhin-fronte kontsekutibo biren arteko distantzia) berbera dela: unitate bat l_e = l_o = 1.

2. Igorlea mugitzen (v_e < v_s)

Lehenik igorlearen abiadura, v_e , uhinen abiadura  medio horretan, v_s, baino txikiago dela suposatuko dugu (v_e < 1).

Egiazta ezazu igorlearen higidura ezkerretik eskumara bada (abiadura positiboak), eskumako behatzaileak neurtutako uhin-luzera unitate bat baino txikiagoa da, eta ezkerreko behatzaileak neurtutako uhin-luzera unitate bat baino handiagoa dela,

• Behatzailea igorlearen eskuman: l_o < l_e

• Behatzailea igorlearen ezkerrean: l_o > l_e

Uhin-luzeraren eta frekuentziaren arteko erlazioa alderantzizkoa denez: l = v/f 

• Behatzailea igorlearen eskuman  f_o > f_e

• Behatzailea igorlearen ezkerrean  f_o < f_e

Uhina soinua bada eskumako behatzaileak entzungo duen soinua zorrotzagoa edo altuagoa da, eta ezkerreko behatzaileak entzungo duen soinua grabeagoa edo baxuagoa. Beste modu batean esanda, behatzaileak entzungo duen soinua igorlea hurbiltzen ari zaionean zorrotzagoa izango da, eta igorlea urruntzen ari zaionean grabeagoa.

Pausu botoia klikatu uhin-fronteak geldiarazteko eta saia zaitez irudia paperean errepikatzen erregela eta konpasa erabilita. Adibidez, igorlearen abiadura v_e = 0.5 kasurako, periodo batean uhin-frontea uhin-luzera bat desplazatu da (unitate bat) eta igorlea ordea, denbora berean uhin-luzera erdia (unitate erdia).

Pausu botoia klikatu behin eta berriro, eta neur ezazu behatzaile bientzat uhin-fronte kontsekutibo biren arteko denbora-tartea, edo periodoa. Neurtutako kantitatearen alderantzizkoa maiztasuna da, bai ezkerreko zein eskumako behatzailearentzat. 

3. Igorlea mugitzen (v_e = v_s)

Konproba ezazu igorlearen abiadura, v_e, uhinen abiaduraren, v_s-ren, berdina denean (v_e = 1), eskumako behatzailearentzat neurtutako uhin-luzera nulua dela. Igorlea hegazkin bat bada, soinuaren abiaduraz mugitzen ari dena, uhin-fronte guztiak hegazkinaren muturrean pilatzen dira. 

4. Igorlea mugitzen (v_e > v_s)

Ikus ezazu igorlearen abiadura, v_e, uhinen abiadura, v_s, baino handiagoa denean (v_e > 1), uhin erresultantea konikoa dela, igorlea bere erpinean duena, uhin-fronte kontsekutiboen inguratzailea delako. Uhin-mota honi talka-uhin edo Mach-en uhin deritzo, eta hegazkin supersonikoek osatzen duten berbera da, bat-bateko soinu bortitza. Itsasontziek ere uraren gainazalean ur-olatuena baino abiadura handiagoaz mugitzen direnean uhara edo estela konikoa uzten dute bere atzean.

2. Behatzailea mugitzen (v_e < v_s  eta  v_o< v_s)

Bai igorlearen eta bai behatzailearen abiadurak, biak, uhinak medio horretan duena baino txikiagoa dela kontsideratuko dugu.

1. Idatzi Igorlearen abiadura bere kontrolean, eta Behatzailearen abiadura dagokion kontrolean. Zenbaki biek unitatea baino txikiagoak izan behar dute, balio absolutuan, baina positiboa igorlearentzat eta negatiboa zein negatiboa behatzailearentzat.

2. Egiazta ezazu igorlea eta behatzailea abiadura berberaz eta noranzko berean mugitzen direnean Doppler efektua ez dela existitzen (abiadura biak erlatiboak idazten ditugulako, hau da, uhinaren abiadurarekiko).

3. Geldi/Jarraitu eta Pausu botoiak erabiliz, neur ezazu behatzaileak bi uhin-fronte kontsekutiboren artean neurtutako denbora, eta konpara ezazu igorleak emititutakoarekin (unitate bat dena). Berdinak al dira bi denborak? 

Ondorengo simulazioan soinu-igorle batek ibilbide zirkularra deskribatzen du, R erradioduna, eta w abiadura angeluar konstanteaz. Hemen behatzailea geldi dago zirkunferentziaren puntu batean eta Doppler-efektua behatuko du.

• Soinu-igorleak deskribatutako zirkunferentziaren R erradioa finkoa da eta unitatetzat hartu da: R = 1.

• Soinuaren abiadura ere unitatean finkatu da:  v_s = 1

• Igorlearen soinuaren frekuentzia f = 4.

Instrukzioak

1. Igorlearen abiadura kontrolean idatz ezazu errotazio-abiadura angeluarra, w,  0 eta 1 bitarteko zenbaki bat.

2. Hasi botoia klikatu.

3. Beha ezazu soinu-igorlearen mugimendua: habe grisaren ertzeko puntu gorria, zirkulu bat deskribatzen ari dena eta bitartean soinua emititzen, gorriz irudikatutako uhin-fronte zirkularrez. Behatzailea geldi dago igorlearen hasierako posizioan puntu urdin batez adierazita.

4. Ikus ezazu uhin-fronte harmonikoaren (gorrien) mozketa igorlea eta behatzailea lotzen dituen zuzenarekin (beltzarekin), gainera leihatilaren beheko aldean xehetasunez erakusten da. Kasu honetan, v_e  ez da igorlearen ωR abiadura osoa, baizik eta abiaduraren proiekzioa igorlea eta behatzailea lotzen dituen zuzenean. Horregatik, behatzaileak jasoko duen frekuentzia, f ', proiekzio horren menpekoa da. Bektoreak irudikatuz adierazten dira igorlearen abiadura (beltza) eta bere proiekzioa (gorria).

5. Behatzaileak jasotako f ' frekuentzia igorlearen q posizio angeluarraren menpe idatz daiteke eta horixe da simulazioaren eskuinaldean adierazten dena, f '  q-ren menpe edo ωt-ren menpe. Egiazta itzazu ondoko kasuak:

• Igorlea behatzailearen kontrako posizioan dagoenean: ωt = (2k+1)π,  k = 0, 1, 2, 3…  frekuentzia f ’= f = 4.

• Igorlea behatzailearen ondotik pasatzen denean: ωt = 2kπ,  k= 0, 1, 2, 3… f ’ frekuentzia maximotik minimora pasatzen da bat-batean.

Uhinen Islapen eta Transmisioa

Ondorengo simulazioan soka bi adierazten dira, masa-dentsitate lineal ezberdinekoak, biak elkarri lotuta koordenatuen jatorrian baina tentsio berberaz. Uhin bat propagatzen ari denean soka batetik bestera pasatzen bada, abiadura aldatzen zaio, baina ez maiztasuna. Lehen eskualdean, zurian, uhin erasotzailea (arrosa) eta islatutakoa (gorria) ikus daitezke, eta bien gainezarmena ere bai (urdina). Bigarren eskualdean, arrosa kolorekoan, transmitituriko uhina bakarrik ikusten da (urdina). Aipatzekoa da mugan, hau da, jatorrian, uhinaren funtzioa jarraia dela.

Simulazioaren azpialdean uhin guztien koloreak azalduta daude.

Instrukzioak

1. Uhinaren maiztasuna Frekuentzia kontrolean idatzi. 

2. Idatz ezazu 1 medioko abiadura kontrolean uhinak ezkerreko medioan duena: v₁ , eta 2 medioko abiadura kontrolean uhinak eskumako medioan duena: v₂ .

3. Hasi botoia klikatu animazioa hasteko.

4. Aipatzekoa da uhin transmititua eta uhin erasotzailea fasean daudela beti, uhin islatua ordea, erasotzailearekin fasean edo fase-oposaketan egon daiteke bigarren medioko abiadura lehenengo mediokoa baino handiagoa bada eta alderantziz.

5. Geldi botoia klikatu animazioa gelditzeko, eta horrela uhin luzerak neur daitezke: erasotzailea, islatua, eta transmititua. Botoi berbera klikatu, Jarraitu izena du orain, animazioa ikusten jarraitzeko. 

6. Pausu botoia klikatuz behin eta berriz, uhinaren nodoak astiro-astiro mugi daitezke erregelaren zenbaki osoetan jartzeko, horrela bere uhin-luzera errazago neurtzeko.

7. Egiazta bedi medio bietako uhin-luzeren arteko erlazioa eta propagazio-abiaduren erlazioa berdinak direla: l₁/l₂ = v₁/v₂

8. Geldi botoia klikatuz animazioa berriro gelditu eta uhinen anplitudeak neurtu: erasotzailea, islatua eta transmititua. 

9. Egiazta ezazu uhin transmitituaren eta erasotzailearen anplitudeen arteko erlazioa hau dela:  2v₂/(v₁ + v₂).

10. Eta egiazta ezazu uhin islatuaren eta erasotzailearen anplitudeen arteko erlazioa hau dela:  (v₁-v₂) / (v₁+v₂).

Errefrakzioa

Ondorengo simulazioan errefrakzioaren Snell-en legea egiazta daiteke. S iturritik irtendako izpi bat P behatzaileraino doa. Lehen tartea, SO tartea alegia, izpiak A medioan zehar deskribatu du v₁ abiaduraz. Bigarren tartea, OP tartea, izpiak B medioan zehar deskribatu du v₂ abiaduraz. Izpiak ibilbide osoa, SOP ibilbidea, betetzeko behar den t denbora, O puntuaren x posizioaren menpekoa da. Eta t(x) funtzioa aztertuz, t-ren deribatua eginez x-ekiko, funtzio horrek minimo bat duela ondorioztatzen da, eta minimo horrek betetzen duen baldintza, hain zuzen, Snell-en errefrakzioaren legearen baliokidea da.

Instrukzioak

1. Idatzi uhinaren abiadura 1 medioan, v₁, A Abiadura kontrolean. Adibidez, v₁ = 1.0.

2. Idatzi uhinaren abiadura 2 medioan, v₂, B Abiadura kontrolean. Adibidez, v₂ = 4.0.

3. Klikatu Berria botoia.

4. Bi puntu aleatorio agertzen dira: S, iturria (puntu urdina goiko aldean) eta P puntua (puntu urdina behealdean). Berria botoia klikatzen dugun bakoitzean posizio ezberdin bi agertzen dira.

5. Marraztu botoia klikatuz SOP bidea marrazten da, eta uhinak tardatuko duen denbora kalkulatu eta goian adierazten da. Hasieran O puntua, mugan dagoen karratu txiki gorria, x=0 posizioan dago.

6. Alda ezazu O puntuaren posizioa, punteroarekin eramanda ezkerrera edo eskumara; Marraztu botoia berriro klikatzean uhinak tardatutako denbora berria idazten da eta aurreko aukerakoa ere bai, biak konparatu ahal izateko. Denbora minimoa duen ibilbidea atzematen denean, hauxe da uhinak benetan jarraituko duen SOP bidea, eraso-angelua eta errefrakzio-angelua irudikatuta agertzen dira eta euren balioak ematen dira.

7. Egiazta ezazu Snell-en legea betetzen dela.

Eraman ezazu punteroarekin karratutxo gorria

Difrakzioa

Difrakzioa eta interferentzia dira uhin fenomeno tipikoenak. Difrakzioa uhinak oztopo bat gainditzen duenean behatutako distortsioa da, baina nabarmena izateko oztopoaren eta uhin-luzeraren tamainak antzekoak izan behar dira. Kasurik sinpleena Fraunhofer-en difrakzioa da, behatzailea oztopoaren ondorenetik eta urruti kokatzen denean. Oztopotzat irekigune estu eta luze bat hartuko da, norabide bateko ertzak bakarrik kontsideratu ahal izateko. Suposatuko dugu uhinak irekigunearen planoaren perpendikularki erasotzen duela.

Huygens-en printzipioaren arabera, uhinak irekigunea atzematen duenean plano horretako puntu guztiak iturri sekundario bihurtzen dira, uhin berriak igorriz. Uhin berrien gainezarmenak uhin-fronte berria osatzen du eta horixe izango da uhin difraktatua. Hortaz, difrakzioa irekigunearen planoan kokatuta dauden infinitu puntuen igorpenen interferentzia edo gainezartzea ere kontsidera daiteke.

Instrukzioak

1. Irekigunearen zabalera aukeratu Irekigunearen Zabalera izeneko desplazamendu barran kurtsorearekin mugituz. Adibidez: 10. 

2. Uhin luzera aukeratu Uhin luzera izeneko desplazamendu barran kurtsorearekin mugituz. Adibidez: 40. 

3. Irekigunearen barnean kontsideratuko diren iturri sekundarioen kopurua hautatu Iturri-kopurua kontrolean; Adibidez: 20. Zenbat eta handiagoa izan iturri sekundarioen kopurua errealagoa izango da lortutako difrakzio-patroia, baina ordenadoreak ere denbora gehiago beharko du kalkuluak burutzeko.

4. Irudia botoia klikatu. Ur-uhinen ontzi bateko argazkia bezalako irudia erakusten da: uhin planoak erakusten dira irekigunearen ezkerretik perpendikularki erasotzen, eta ondoren, difraktatutako uhina. Eskumarago eta goitik behera, grisen eskalan adierazita, x=200 posizioko intentsitatea (ur-uhinen ontziaren bukaeran) intentsitate maximoa zuriz eta nulua beltzez. Eskuinean intentsitate berorren adierazpen grafikoa posizio bertikalaren menpe.

5. Kontutan izan Fraunhofer-en difrakzioan behatzailea urruti egon behar dela irekigunearen tamainarekin konparatuta, eta simulazio honetan baldintza hau ez da ondo betetzen. Hala ere, gure helburu nagusia ez da difrakzioaren minimoak zehaztasunez kalkulatzea, horren ordez, erakutsi nahi duguna da funtsean difrakzioa eta interferentzia fenomeno bera direla.

GALDERAK

a Soinu-uhinen maiztasuna txikiagotu egiten da, igorlea eta hartzailea

1. medioarekiko pausagunean daudenean

2. hurbiltzen direnean

3. urruntzen direnean

4. medioarekiko mugitzen daudenean

b Horma batek zurgatutako intentsitatea,

1. uhin erasotzailearen intentsitatearen eta islatutako intentsitatearen batura.

2. uhin erasotzailearen intentsitatearen eta islatutako intentsitatearen kendura.

3. uhin erasotzailearen intentsitatearen eta disipatutako intentsitatearen kendura.

4. uhin erasotzailearen intentsitatearen eta disipatutako intentsitateen kendura

c Errefrakzioan, Snell-en legearen arabera:

1. eraso eta errefrakzio angeluak ezberdinak dira.        

2. eraso eta errefrakzio angeluak berdinak dira.

3. eraso eta errefrakzio angeluen sinuen zatidura 1 da.

4. islapen eta errefrakzio angeluak berdinak dira.

d Hizlariak ikusi gabe ere, elkarrizketa bat leiho ireki batean zehar entzutea posiblea da,  honako fenomenoaren bidez:

1. oihartzuna

2. erreberberazioa

3. absortzioa

4. difrakzioa

e Bibrazio bat iturri bibratzaile batetik medio batera transmititzen da ondoko fenomenoaren bidez:

1. erradiazioa                                                            

2. absortzioa                                           

3. difrakzioa                                                                

4. errefrakzioa

  Emaitzak: a3     b2     c1     d4    e1  

MULTIMEDIA ETA WEB BALIABIDEAK

Gai honetaz gehiago irakurri nahi baduzu, ondoko estekan erreferentziak aurkituko dituzu:   , eta gero honako atalean  .