Diferencia entre revisiones de «Statistical Parametric Mapping»
Sin resumen de edición |
Sin resumen de edición |
||
| (No se muestran 5 ediciones intermedias del mismo usuario) | |||
| Línea 1: | Línea 1: | ||
== Topological inference and the theory of random fields == | |||
<center>[[Imagen:Random_Field_Theory_SPM.png]]</center> | <center>[[Imagen:Random_Field_Theory_SPM.png]]</center> | ||
Information | Schematic illustrating the use of Random Field Theory in making inferences about SPMs. If one knew precisely where to look, then inference can be based on the value of the statistic at the specified location in the SPM. However, generally, one does not have a precise anatomical prior, and an adjustment for multiple dependent comparisons has to be made to the p-values. These corrections use distributional approximations from RFT. This schematic deals with a general case of n SPM{t} whose voxels all survive a common threshold u (i.e. a conjunction of n component SPMs). The central probability, upon which all peak, cluster or set-level inferences are made, is the probability P(u,c,k) of getting c or more clusters with k or more RESELS (resolution elements) above this threshold. By assuming that clusters behave like a multidimensional Poisson point-process (i.e., the Poisson clumping heuristic), P(u,c,k) is determined simply: the distribution of c is Poisson with an expectation that corresponds to the product of the expected number of clusters, of any size, and the probability that any cluster will be bigger than k RESELS. The latter probability depends on the expected number of RESELS per cluster \eta. This is simply the expected supra-threshold volume, divided by the expected number of clusters. The expected number of clusters \psi_0 is estimated with the Euler characteristic (EC) (effectively the number of blobs minus the number of holes). This depends on the EC density for the statistic in question (with degrees of freedom \nu) and the RESEL counts. The EC density is the expected EC per unit of D-dimensional volume of the SPM where the volume of the search is given by the RESEL counts. RESEL counts are a volume measure that has been normalized by the smoothness of the SPMs component error fields (\epsilon), expressed in terms of the full width at half maximum (FWHM). In this example equations for a sphere of radius \epsilon are given. \Psi denotes the cumulative density function for the statistic in question. | ||
== Reference == | |||
Information copied from [http://www.scholarpedia.org/article/Statistical_parametric_mapping_(SPM) here] | |||
== More info == | |||
[http://www.ehu.es/ccwintco/uploads/4/4c/Spm-rft-slides-poirrier06.pdf Random Field Theory on fMRI] | |||
Revisión actual - 16:02 13 ene 2009
Topological inference and the theory of random fields
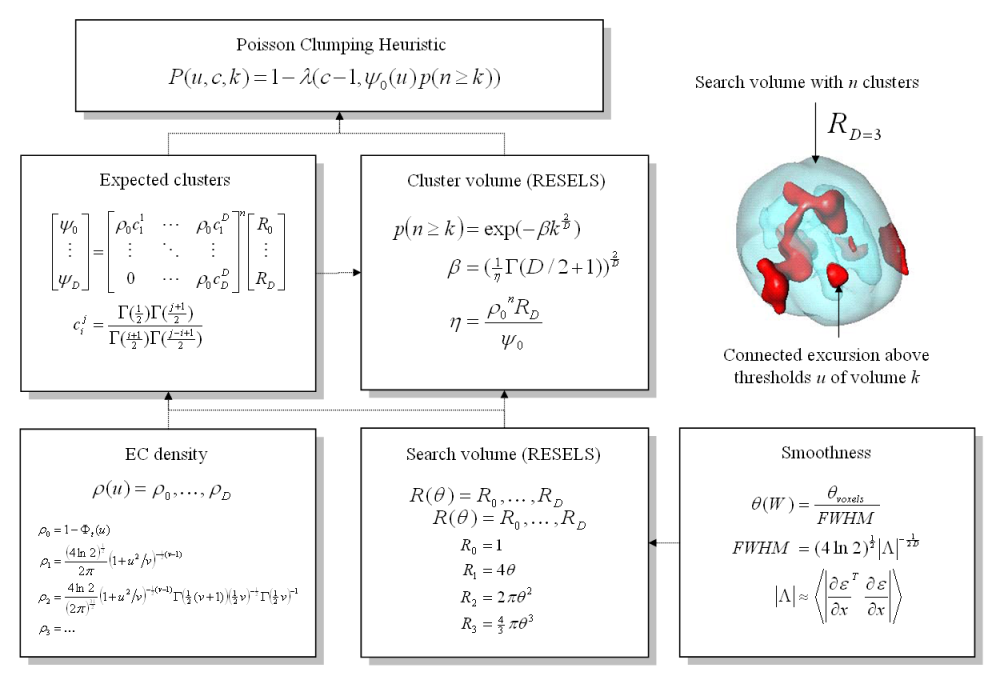
Schematic illustrating the use of Random Field Theory in making inferences about SPMs. If one knew precisely where to look, then inference can be based on the value of the statistic at the specified location in the SPM. However, generally, one does not have a precise anatomical prior, and an adjustment for multiple dependent comparisons has to be made to the p-values. These corrections use distributional approximations from RFT. This schematic deals with a general case of n SPM{t} whose voxels all survive a common threshold u (i.e. a conjunction of n component SPMs). The central probability, upon which all peak, cluster or set-level inferences are made, is the probability P(u,c,k) of getting c or more clusters with k or more RESELS (resolution elements) above this threshold. By assuming that clusters behave like a multidimensional Poisson point-process (i.e., the Poisson clumping heuristic), P(u,c,k) is determined simply: the distribution of c is Poisson with an expectation that corresponds to the product of the expected number of clusters, of any size, and the probability that any cluster will be bigger than k RESELS. The latter probability depends on the expected number of RESELS per cluster \eta. This is simply the expected supra-threshold volume, divided by the expected number of clusters. The expected number of clusters \psi_0 is estimated with the Euler characteristic (EC) (effectively the number of blobs minus the number of holes). This depends on the EC density for the statistic in question (with degrees of freedom \nu) and the RESEL counts. The EC density is the expected EC per unit of D-dimensional volume of the SPM where the volume of the search is given by the RESEL counts. RESEL counts are a volume measure that has been normalized by the smoothness of the SPMs component error fields (\epsilon), expressed in terms of the full width at half maximum (FWHM). In this example equations for a sphere of radius \epsilon are given. \Psi denotes the cumulative density function for the statistic in question.
Reference
Information copied from here