DESKRIBAPENA

Demagun osziladore ilara bat, denak akoplatuak, honela bata higitzean inguruko beste guztiek ere eragina nabaritzen dute. Osziladore bi edo gehiago akoplatuta daudela esaten da energia-elkartruke dezaketenean. Uhin-higidura existitzen da, sistema bibratorioak, elkarrengandik hurbil egonda, batetik bestera energia transmititzeko gai direlako.

Osziladore biren arteko energia-transferentzia gertatzen da, bi osziladoreek elementuren bat konpartitzen dutelako (zurruntasuna, masa, erresistentzia...). Erresistentzia-bidezko akoplamenduak nahitaez energia-galera suposatzen du eta hortaz, bibrazioa moteltzea. Zurruntasun edo masa bidezko akoplamenduek ordea, ez dute potentziarik kontsumitzen, eta honela osziladore baten energia beste guztietara transferi daiteke. Hauxe da uhin higiduraren oinarria.

Demagun, adibide gisa, ondoko sistema mekanikoa: partikula bi, m masadunak, biak k konstantedun malgukiz hormara lotuta, eta euren artean beste k_c malguki bat.

Osziladore akoplatu bi

Osziladore akoplatu biren bibrazio-modu normalak

Osziladore akoplatuetan badaude higidura-mota berezi batzuk: partikula biak frekuentzia berarekin oszilatzen dutenean eta fase-diferentzia konstantea denean, bibrazio-modu normala deritzo.

Malguki eta partikula-sistema baten bibrazio-modu normalak

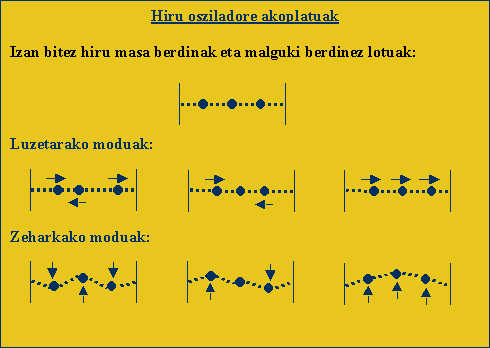
Kontsideratu dugun sistema oszilatorioan, bi masa eta hiru malguki genituen. Sistema honek bibrazio-modu normal bi ditu luzetara eta beste bi zabaletara (masak malgukiekiko perpendikularki higitzen direnean). Bi kasuetan, luzetara eta zabaletara, bibrazio-modu bat agertzen da, frekuentzia baxuaz, masa biak noranzko berean higitzen, eta beste bibrazio-modu bat, frekuentzia altuaz, masa biak kontrako noranzkoez higitzen.

Emaitza hau partikula gehiago dituen sistema batean aplikatu nahi badugu, antzeko emaitzak aurkituko ditugu: sistemak hiru masa baditu, planoan higi daitezkeenak, hiru bibrazio-modu ditu luzetara eta beste hiru zabaletara..

Masa eta malgukien kopurua handitzen badugu, bibrazio-moduen kopurua ere handituko da: gehitzen den masa berri bakoitzeko bibrazio-modu berri bat agertzen da luzetara eta beste bat zabaletara. Horregatik orokorrean, N masa ditugunean malguki identikoez lotuta, N bibrazio-modu dituzte luzetara eta beste N zabaletara.

Partikula- eta malguki-sistema baten oszilazio behartuak

Aurreko atalean, sistema baten oszilazio-modu normal ezberdinak aurkeztu ditugu. Modu horiek exzitatzeko indar harmoniko bat aplika daiteke, F_o anplitudeaz eta w_f  frekuentziaz. Laborategiko praktika batean egin daiteke, masa batzuk malgukiez lotu, eta bibrazioak behartzeko, lehenengo masa soka batez disko birakor baten ertzean lotu eta diskoari abiadura angeluar aldakorra duen motor batekin eragin. Lortzen den sistemaren oszilazioak behatuz, aplikaturiko indar oszilakorraren frekuentzia sistemaren modu normal baten berdina denean, orduantxe oszilatzen du sistemak modu normal horretan, eta sistema erresonantzian dagoela esaten da.

Uhin mekanikoak eta uhin harmonikoak

Malgukien bitartez lotutako masa-kopurua handitzen doan heinean, sistema osoak linealagoa eta jarraikiagoa dirudi, partikula bakoitzaren izaera gero eta gutxiago nabarmentzen delako. Medio horren elastikotasuna aprobetxatuz, perturbazio bat propagatu egin daiteke medio horretan zehar uhin mekanikoaren kontzeptua sortuz. Eredu sinple honetan, medio materialeko materia, partikulen bitartez adierazita dago, eta bere elastikotasuna malgukien bitartez. Lehenengo partikula bere oreka-posiziotik luzetara desplazatzen denean, eta gero aske utzi, bere desplazamendua bigarren partikulara transmititzen da, eta bigarrenetik hirugarrenera, eta abar, bakoitzak bere ondorengoari transmitituz. Higidura guzti honen emaitza luzetarako pultsu baten transmisioa da. Malgukiz lotutako partikulen luzetarako higidurak, ba du antzik, materiaren higidurarekin, luzetarako uhin bat propagatzen ari denean. Partikulak, luzetara desplazatu beharrean, zabaletara desplazatzen direnean, medioan zehar propagatzen ari den uhina zabaletarakoa da, eta badaude beste kasu batzuk, ez direnak erabat luzetara ezta erabat zabaletara, bien nahasketa baizik, adibidez likidoen gainazaleko uhinak (olatuak...).

Oreka-posizioarekiko perturbazio bat gertatzen bada posizio batean, energia-gehigarri bat agertu dela esan nahi du. Hortaz, perturbazioa propagatzen bada, energia garraiatuko da medio material horretan zehar, baina materia bera garraiatu gabe.

Uhinak medio materialean zehar duten propagazio-abiadura, medioaren beraren elastikotasunaren eta dentsitatearen menpekoa da. Uhinen propagazio-abiadura berdina bada edozein frekuentziadun uhinentzat, medioa ez-dispertsiboa dela esaten da, eta alderantziz, uhinen propagazio-abiadura uhinaren beraren frekuentziaren menpekoa bada, medioa dispertsiboa dela esaten da.

ADIBIDE ETA SIMULAZIOAK

Osziladore akoplatu bi

Ondorengo simulazioak, partikula akoplatu biren oszilazioa erakusten du. Bertan ikus daiteke, osziladore baten anplitudea anulatzen dela bestearena maximoa denean eta alderantziz, eta elkarrekintza honek tardatzen duen denbora neurtu. Leihatilaren goiko ezkerraldean denboraren zenbakizko balioa ematen da, eta behealdean, partikula bakoitzaren posizioa denboraren menpe.

Instrukzioak

• Malgukien kontrolean, Malgukien k , konstantearen balioa idatzi behar da: adibidez 10.

• Akoplamenduaren kontrolerako, Akoplamenduaren k, bitarteko malgukiaren konstantea idatzi behar da, adibidez 0.5. Partikulen masak unitarioak hartu dira, hau da, 1.

• Hasierako posizioaren kontrolean, 1-en hasierako posizioa, ezkerreko partikularen hasierako posizioa idatzi behar da: bat baino txikiagoa edo berdina. Eskumako partikularen hasierako posizioa, 2-ren hasierako posizioa, kontrolean idatzi. Kasu guztietarako hasierako abiadurak nuluak hartu dira.  Adibidez, idatz bedi 1-en hasierako posizioa, 1.0, eta 2-ren hasierako posizioa, 0.0.

• Parametroak kontrol guztietan idatzi ondoren Hasi botoia klikatu animazioari ekiteko. Edozein momentutan geldi daiteke Geldi botoia klikatuz. Animazioa jarraitzeko botoi bera klikatu, baina orain bere izena Jarraitu da. Sistemaren portaera astiroago aztertzeko, hau da, pausoka, Pausu botoia klikatu, pausu bakoitzerako behin. Berriro animazioa abiatu nahi bada, berriz klikatu Jarraitu botoia.

• Erabil bitez Geldi eta Pausu botoiak osziladoreetako bat gelditzen den aldiunera pausoka hurbiltzeko. Frekuentzia angeluarrak teorikoki ere kalkula daitezke, w_b eta w_a , eta anplitude modulatuaren frekuentzia ere bai: (w_a - w_b )/2 . Eta beraietatik periodoak. Gero, balio teorikoak eta neurtutakoak konpara daitezke.

• Bibrazio-modu normalak lortzeko:

1. Lehen modu normala lortzeko, sar bedi kantitate berbera hasierako posiziorako bi kontroletan. Adibidez, Hasierako posizioa: 1.0 bientzat. 

2. Bigarren modu normala lortzeko, sar bedi kantitate berbera, baina kontrako zeinuaz, hasierako posiziorako bi kontroletan. Adibidez, 1-en hasierako posizioa: 1.0 eta 2-ren hasierako posizioa: –1.0.

N osziladore akoplaturen bibrazio-modu normalak

Ondorengo simulazioan, N partikula eta malgukiren higidura erakutsiko da, bibratzen, "luzetarako bibrazio-modu normaletan". Leihatilaren goiko aldean, n modu posibleetatik, aukeratutako modu normalaren zenbakia erakusten da, n, alegia, eta bere frekuentzia w_n.  Simulazioaren beheko aldean, grafiko batean, ardatz bertikalean, partikula bakoitzaren desplazamendua.  Ariketa bezala, gomendagarria da, grafiko batean adieraztea, frekuentziaren balioa  uhin zenbakiaren menpe (hau da, n, moduaren zenbakiaren menpe).

Instrukzioak

• Partikula kopurua kontrolean, sistemaren partikula kopurua idatzi (bi baino gehiago).

• Malgukiaren konstantea kontrolean malgukiaren konstantea idatzi. Malguki guztiak berdinak hartzen dira.

• Hurrengoa>> kontrolean klikatuz bibrazio-modu batetik hurrengora pasatzen da: n-garrenetik (n+1)garrenera.

• Aurrekoa<< kontrolean klikatuz aurreko bibrazio-modura pasatzen da.

Partikula- eta malguki-sistema baten oszilazio behartuak

Simulatuko dugun laborategiko praktika honetan, partikula-multzo bat, malgukien bitartez lotuta daukagu. Lehenengo pendulua, hari batez disko birakor baten ertzean lotu eta diskoari abiadura angeluar aldakorra duen motor batekin eragin. Lortzen diren oszilazioak, partikula- eta malguki-sistema baten oszilazio behartuak dira. 

Instrukzioak

• Partikula-kopurua kontrolean, sistemako partikula kopurua idatzi; bi baino gehiago.

• Malgukiaren konstantea kontrolean, idatz ezazu malgukien konstantea (denak berdinak direla suposatzen da). 

• Frekuentzia angeluarra kontrolean, aplikatzen den indar harmoniko behartzailearen frekuentzia idatzi.

• Indar Harmonikoa kontrolean, aplikatzen den indar harmoniko behartzailearen anplitudea idatzi.

• Sistemaren bibrazio-modu normalak ikusteko, aplikatzen den Frekuentzia angeluarra, kontrolean bibrazio-modu konkretu bati dagokion frekuentzia idatzi behar da, eta sistemak horrelaxe oszilatuko du. 

• Oszilazioen anplitudea handitu edo gutxitzeko, aplikaturiko indarraren anplitudea kontrola daiteke Indar harmonikoa kontrolaren bitartez.

• Beha itzazu sistemaren oszilazioak, erresonantziazkoak ez diren beste frekuentzia batzuekin. Bereziki, lehenengo bibrazio-modua baino frekuentzia txikiagoak direnean, eta azkenengo bibrazio-modua baino frekuentzia altuagoak direnean.

Uhin mekanikoak

Ondorengo simulazioan, kopuru handiko partikula- eta malguki sistema baten higidura aztertuko dugu, lehen partikula bere oreka-posiziotik desplazatu eta bat-batean askatzen denean, hau da, luzetarako pultsu baten propagazioa. Gauza bi neurtuko dira: alde batetik, pultsuak sistemako azken muturreko partikulara heldu arte tardatzen duen denbora, eta bestetik, propagazio-abiadurak malgukien konstantearekin duen erlazioa, kualitatiboki. Partikulen higidura hobeto ikusteko, leihatilaren behealdean, partikulen desplazamendua erakusten da denboran zehar. 

Instrukzioak

• Partikula-kopurua kontrolean, sistemako partikula kopurua idatzi; adibidez 20.

• Malgukiaren konstantea kontrolean, idatz ezazu malgukien konstantea (denak berdinak direla suposatzen da). Adibidez 0.5.

• Simulazioa hasteko Hasi botoia klikatu.

• Leihatilaren goiko ezkerraldean, denbora adierazten da, lehen partikula desplazatu eta askatu denetik, eta ondoan, azken partikularen posizioa denboraren menpe.

• Lehen partikularen desplazamendua, askatzen denean, unitatetzat hartu da. Pultsua azken partikularaino iritsi dela esan dezakegu, azken partikularen desplazamendua, adibidez, 0.3 baino handiagoa denean, balio absolutuan. Neur ezazu denbora.

• Malgukiaren konstantea aldatu egin daiteke, adibidez, 1.0. Propagazio-abiadura aldatzen ote da? Hau da, muturreko partikulara iristeko denbora txikiagoa da ala handiagoa?

• Pausa botoia klikatu, simulazioa unetxo batez gelditzeko eta zenbakizko balioak hobeto irakurri ahal izateko. Aurrera jarraitzeko botoi bera klikatu, baina orain Jarraitu izena du.

• Pausu botoia behin eta berriz klikatuz, sistemaren portaera pausoka ere azter daiteke.

GALDERAK

a Osziladore akoplatu bi modu normal batean bibratzen ari dira: partikuletako baten higiduraren frekuentzia:

1. bestearen higiduraren frekuentziaren doblea da.

2. bestearen higiduraren frekuentziaren erdia da.

3. bestearen higiduraren frekuentziaren berbera da.

4. bestearen higiduraren frekuentziaren ezberdina da.

b Osziladore akoplatu bi, luzetarako modu normal batean bibratzen ari direnean:

1. fasean daude                                                        

2. fase-oposizioan daude                                                       

3. edo fasean edo fase-oposizioan egon daitezke.                                                            

4. Ez fasean ezta fase-oposizioan ere ez.

c Objektu baten bibrazioen berezko frekuentzia 4 Hz da. Hortaz, ondoko frekuentziez erresonantziak ditu:

1. 1 Hz 

2. 2 Hz             

3. aurreko bietan 

4. 16 Hz

d N osziladore akoplatuko sistema batean, luzetarako modu normalen kopurua:               

1. zabaletarako modu normalen kopuru bera da                                                                         

2. zabaletarako modu normalen kopuruaren alderantziz proportzionala da.                  

3. zabaletarako modu normalen kopuru ezberdina da    

4. zabaletarako modu normalen kopurua gehi bat-en erro karratuaren zuzenki proportzionala da. 

e Medio dispertsibo batean, uhinen propagazio-abiadura: 

1. frekuentzia guztietarako berbera da.                                                           

2. frekuentzia ezberdinetarako, ezberdina da.                                            

3. ez da medioaren araberakoa.                                                                

4. nulua da

  Emaitzak:  a3   b3   c4   d1   e2  

MULTIMEDIA ETA WEB BALIABIDEAK

Gai honetaz gehiago irakurri nahi baduzu, ondoko estekan erreferentziak aurkituko dituzu:   , eta gero honako atalean  .