DESCRIPCIÓN

Suponemos varios osciladores acoplados de forma que el movimiento de uno de ellos influye en todos los demás. El efecto neto del acoplamiento de dos o más osciladores se puede describir como un intercambio de energía entre ellos. El movimiento ondulatorio debe su existencia a sistemas vibrantes próximos que son capaces de transmitir su energía unos a otros.

La transferencia de energía entre dos osciladores se debe a que ambos comparten un elemento (rigidez, masa o resistencia). El acoplamiento de resistencia inevitablemente conlleva pérdida de energía y por lo tanto un rápido decaimiento de la vibración. Sin embargo, el decaimiento vía rigidez o masa no consume potencia, siendo posible la transferencia continua de energía entre muchos osciladores, lo que constituye la base del movimiento ondulatorio.

Consideremos como ejemplo un sistema mecánico con acoplamiento de rigidez: dos partículas iguales de masa m unidas, cada una de ellas, a un muelle de constante elástica k, y acopladas a través de un tercer muelle de constante k_c.

Dos osciladores acoplados

Modos normales de vibración de dos osciladores acoplados

Los modos normales de vibración son casos especiales del movimiento de osciladores acoplados. Corresponden al caso en el que las dos partículas se mueven con la misma frecuencia y mantienen una diferencia de fase constante.

Modos normales de vibración de un sistema de muelles y partículas

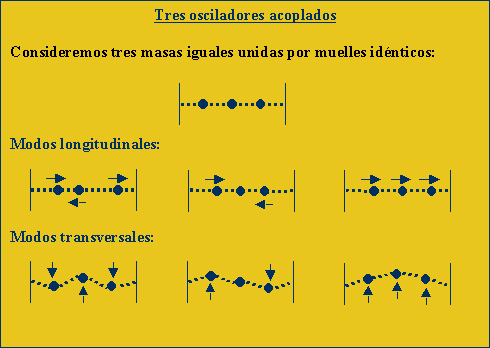
Hasta ahora hemos considerado un sistema oscilante compuesto por dos masas y tres muelles. Este sistema presenta dos modos longitudinales de vibración y también dos transversales (movimiento de las partículas perpendicular a la línea de los muelles). En ambas parejas, longitudinal y transversal, aparece un modo de baja frecuencia en el que las masas se mueven en la misma dirección, y un modo de alta frecuencia en el que las masas se mueven en direcciones opuestas.

Si intentamos generalizar estos resultados para el caso de sistemas con un mayor número de masas, encontramos resultados similares: para el sistema de tres masas que sólo puede moverse en un plano aparecen tres modos longitudinales y tres normales.

Si aumentamos el número de masas y muelles en nuestra distribución lineal aumenta también el número de modos normales: para cada masa que se añade aparece un nuevo modo longitudinal y otro transversal. De esta forma podemos generalizar diciendo que un conjunto de N masas iguales unidas por muelles idénticos y que puede vibrar en un plano, tiene N modos normales longitudinales y N transversales.

Oscilaciones forzadas de un sistema de muelles y partículas

En la sección anterior, hemos considerado los distintos modos normales de vibración de un sistema. En ésta, consideramos cómo se excitan aplicando una fuerza oscilante de amplitud F_o y frecuencia angular w_f. Este es el caso de una experiencia de laboratorio que consiste en un sistema de péndulos que unimos mediante muelles. El primero, lo unimos mediante una cuerda a una punta clavada en la periferia de un disco que gira accionado por un motor de velocidad variable. La situación que se describe corresponde a las oscilaciones forzadas de un sistema formado por partículas y muelles. Se excita un determinado modo de vibración siempre que la frecuencia de la fuerza oscilante sea igual a la frecuencia de dicho modo de vibración. Se dice entonces que  el sistema  está en resonancia.

Ondas mecánicas y ondas armónicas

Cuando el número de masas de nuestro sistema lineal aumenta, éste se nos aparece como un sistema unidimensional continuo, ya que notamos cada vez menos cada elemento individual. Podemos introducir el concepto de onda mecánica como la propagación de una perturbación en un medio material, aprovechando las propiedades elásticas de dicho medio. En este sencillo modelo, las partículas del medio están representadas por las masas, mientras que sus propiedades elásticas vienen representadas por los muelles. Cuando la primera partícula se desvía longitudinalmente de su posición de equilibrio y a continuación se suelta, su movimiento se transmite a la segunda partícula y de ésta a la tercera, y así sucesivamente. El resultado es la propagación de un pulso longitudinal. El movimiento longitudinal de las masas tiene semejanza con el de las partículas de un medio material en el se propaga una onda longitudinal. En el caso de que las masas se desplazaran transversalmente el movimiento que percibiríamos sería semejante a la propagación de una onda transversal en el medio material. Existen otros casos en los que los movimientos de las partículas del medio no son ni puramente longitudinales ni transversales (por ejemplo las ondas superficiales en un líquido).

Cualquier perturbación respecto al equilibrio de un sistema supone una energía adicional localizada en la región del sistema en la que se encuentra la perturbación. En consecuencia, la propagación de la perturbación va unida al transporte de energía a través del medio sin transporte neto de materia.

La velocidad con la que las ondas se propagan en un medio depende de las características de dicho medio. Cuando la velocidad de propagación de las ondas es la misma para todas las frecuencias se dice que el medio es no dispersivo para esas ondas. En el caso contrario, cuando la velocidad de propagación depende de la frecuencia el medio es dispersivo.

EJEMPLOS Y SIMULACIONES

Dos osciladores acoplados

La siguiente simulación permite observar las oscilaciones de las dos partículas y medir el tiempo que tarda un oscilador desde que su amplitud se hace cero hasta que vuelve a hacerse cero. En la parte superior izquierda de la ventana de la simulación se da el valor del tiempo, y en la parte inferior se representa el desplazamiento de cada partícula en función del tiempo.

Instrucciones

• En el control de edición titulado k de los muelles se introduce la constante elástica de los osciladores, por ejemplo 10.

• En el control de edición titulado k del acoplamiento se introduce la constante elástica del muelle central, por ejemplo 0.5. La masa de las partículas se ha tomado como la unidad.

• En el control de edición titulado Posición inicial de 1, se introduce la posición inicial de la partícula de la izquierda, una cantidad menor o igual que la unidad. Se introduce la posición inicial de la partícula de la derecha en el control de edición titulado Posición inicial de 2. En todos los casos, las velocidades iniciales se toman como cero. Por ejemplo, introducir en el control de edición titulado Posición inicial 1, la cantidad de 1.0, e introducir en el control de edición titulado Posición inicial 2, la cantidad de 0.0.

• Una vez introducidos los parámetros en los controles de edición respectivos, se pulsa en el botón titulado Empieza, para comenzar la animación. Se puede detener en cualquier momento pulsando en el botón titulado Pausa. Se continúa la animación pulsando en el mismo botón cuyo título ha cambiado a Continua. Para examinar el comportamiento del sistema paso a paso, se pulsa varias veces en el botón titulado Paso. Se continúa la animación pulsando en el botón titulado Continua.

• Usar los botones Pausa y Paso, para aproximarse a los instantes en los que el oscilador elegido se detiene momentáneamente. Pueden calcularse las frecuencias angulares w_b y w_a y la frecuencia angular de la amplitud modulada (w_a - w_b )/2, el periodo y el semiperiodo y comparar el resultado obtenido con las medida efectuada

• Modos normales de vibración:

1. Primer modo normal de oscilación: introducir la misma cantidad, por ejemplo, 1.0 en los controles de edición titulados Posición inicial.

2. Segundo modo normal: introducir la misma cantidad pero con signos opuestos en dichos controles de edición, por ejemplo, 1.0 en Posición inicial 1, y –1.0 en Posición inicial 2.

Modos normales de vibración de dos osciladores acoplados

En la siguiente simulación se van a mostrar de forma animada el movimiento de un sistema formado por partículas y muelles en el modo normal longitudinal de vibración seleccionado. En la parte superior de la ventana, se indica el modo normal de vibración  n  que se representa y su frecuencia w_n. En la parte inferior de la simulación, se representa en el eje vertical el desplazamiento de cada una de las partículas. Como ejercicio se recomienda representar gráficamente, la frecuencia de los distintos modos en función del número de onda (o del número del modo n).

Instrucciones

• En el control de edición titulado Número de partículas introducir el número de partículas del sistema, un número mayor que 2.

• En el control de edición titulado Constante del muelle introducir la constante del muelle.

• Pulsar en el botón titulado Siguiente>> para observar el siguiente modo de vibración.

• Pulsar en el botón titulado Anterior<< para observar el modo de vibración previo.

Oscilaciones forzadas de un sistema de muelles y partículas

Vamos a simular una experiencia de laboratorio que consiste en un sistema de péndulos que unimos mediante muelles. El primero, lo unimos mediante una cuerda a una punta clavada en la periferia de un disco que gira accionado por un motor de velocidad variable. La situación corresponde a las oscilaciones forzadas de un sistema formado por partículas y muelles.

Instrucciones

• En el control de edición titulado Número de partículas introducir el número de partículas del sistema, un número mayor que 2. 

• En el control de edición titulado Constante del muelle introducir la constante del muelle.

• En el control de edición titulado Frecuencia angular introducir la frecuencia de la fuerza oscilante.

• En el control de edición titulado Fuerza oscilante introducir la amplitud de la frecuencia oscilante.

• Observar cómo se excitan los distintos modos normales de vibración del sistema introduciendo en el control de edición Frecuencia angular, el valor de la frecuencia del modo normal de vibración que se desea excitar.

• Ajustar la amplitud de las oscilaciones, disminuyendo o aumentando la amplitud  de la fuerza oscilante, mediante el control de edición Fuerza oscilante.

• Observar el comportamiento del sistema para otras frecuencias que no sean las de resonancia. En particular, frecuencias que estén por debajo de la frecuencia del primer modo, y frecuencias que estén por encima del modo de vibración más alto.

Ondas mecánicas

En la siguiente simulación vamos a examinar el comportamiento de un sistema de muchas partículas y muelles, cuando la primera partícula se desvía longitudinalmente de su posición de equilibrio y a continuación se suelta, es decir, la propagación de un pulso longitudinal. Se intentará determinar el tiempo que tarda el pulso en llegar a la última partícula del sistema y comprobar cualitativamente la dependencia de la velocidad de propagación del pulso en función de la constante elástica del muelle. Para apreciar mejor el movimiento de las partículas en la parte inferior de la ventana de la simulación se representa el desplazamiento de las mismas en función del tiempo.

Instrucciones

• En el control de edición titulado Número de partículas se introduce el número de partículas, por ejemplo, 20.

• En el control de edición titulado Constante del muelle se introduce la constante del muelle, por ejemplo, 0.5.

• Se pulsa el botón titulado Empieza para comenzar la experiencia

• En la esquina superior izquierda de la ventana, leer el tiempo, desde el momento en el que se desplazó la primera partícula y se soltó, y el desplazamiento de la última partícula en función del tiempo.

• La primer partícula se desplaza una unidad. Podemos decir que el pulso ha llegado a la última partícula cuando su desplazamiento sea por ejemplo, mayor o igual a 0.3 en valor absoluto.

• Se cambia la constante del muelle, a un valor, por ejemplo de 1.0. ¿se modifica la velocidad de propagación?, es decir, ¿el tiempo medido es mayor o menor?.

• Pulsar el botón titulado Pausa para parar momentáneamente la animación. Pulsar en el mismo botón titulado ahora Continua para reanudarla.

• Pulsar varias veces en el botón titulado Paso, para examinar el comportamiento del sistema paso a paso.

CUESTIONES

a Dos osciladores acoplados se mueven en un modo normal. La frecuencia a la que se mueve una de las partículas

1. es el doble de la frecuencia a la que se mueve la otra

2. es la mitad de la frecuencia a la que se mueve la otra

3. es igual a la frecuencia a la que se mueve la otra

4. es diferente de la frecuencia a la que se mueve la otra

b En un modo normal longitudinal de dos osciladores acoplados, los dos osciladores se mueven

1. en fase                                                        

2. en oposición de fase                                                       

3. en fase o en oposición de fase                                                            

4. ni en fase ni en oposición de fase

c Un objeto tiene una frecuencia propia de 4 Hz. Por lo tanto, resonará a una frecuencia de 

1. 1 Hz 

2. 2 Hz             

3. a las dos anteriores 

4. 16 Hz

d Para un conjunto de N osciladores acoplados el número de modos normales longitudinales                

1. es igual al número de modos transversales                                                                         

2. es inversamente proporcional al número de modos transversales                   

3. es diferente del número de modos transversales   

4. es directamente proporcional a la raíz cuadrada del número de modos transversales más uno

e En un medio dispersivo la velocidad de propagación de las ondas

1. es la misma para todas las frecuencias                                                           

2. es diferente para las distintas frecuencias                                            

3. no depende del medio                                                                

4. es nula

  Soluciones:  a3   b3   c4   d1   e2  

RECURSOS MULTIMEDIA Y WEB

Si desea ampliar sus conocimientos, pueden resultarle útiles los recursos que se encuentran referenciados en el apartado del enlace