|
|
|
|
movimiento
armónico
simple
y
oscilador
amortiguado
|
|
|
OBJETIVOS
-
Conocer
las características generales de los movimientos oscilatorios.
-
Definir
el movimiento armónico simple.
-
Definir
el oscilador amortiguado.
-
Entender
qué ocurre con la energía en ambos osciladores.
|
DESCRIPCIÓN
Al
observar la Naturaleza nos damos cuenta de que muchos procesos físicos
(por ejemplo la rotación de la tierra en torno al eje polar) son
repetitivos, sucediéndose los hechos cíclicamente tras un intervalo de
tiempo fijo. En estos casos hablamos de movimiento periódico y lo
caracterizamos mediante su período, que es el tiempo necesario para un
ciclo completo del movimiento, o su frecuencia, que representa el número
de ciclos completos por unidad de tiempo.
Un
caso interesante de movimiento periódico aparece cuando un sistema físico
oscila alrededor de una posición de equilibrio estable. El sistema
realiza la misma trayectoria, primero en un sentido y después en el
sentido opuesto, invirtiendo el sentido de su movimiento en los dos
extremos de la trayectoria. Un ciclo completo incluye atravesar dos veces
la posición de equilibrio. La masa sujeta al extremo de un péndulo o de
un resorte, la carga eléctrica almacenada en un condensador, las cuerdas
de un instrumento musical, y las moléculas de una red cristalina son
ejemplos de sistemas físicos que a menudo realizan movimiento oscilatorio.
El
caso más sencillo de movimiento oscilatorio se denomina movimiento armónico
simple y se produce cuando la fuerza resultante que actúa sobre el
sistema es una fuerza restauradora lineal. El Teorema de Fourier nos da
una razón de la importancia del movimiento armónico simple. Según este
teorema, cualquier clase de movimiento periódico u oscilatorio puede
considerarse como la suma de movimientos armónicos simples.
|
|
Movimiento
armónico simple
Consideremos como ejemplo de sistema que describe un movimiento armónico simple una
masa m unida al extremo de un muelle elástico de constante k, como se
muestra en la figura. El otro extremo del muelle está fijo. El movimiento
horizontal de la masa puede describirse utilizando la segunda ley de
Newton: la única fuerza que actúa sobre la masa es la fuerza
recuperadora del muelle, que es proporcional y de sentido opuesto a su
alargamiento x desde una posición de equilibrio estable.
|
|

|
|
Oscilador
amortiguado
Todos
los osciladores reales están sometidos a alguna fricción. Las fuerzas de
fricción son disipativas y el trabajo que realizan es transformado en
calor que es disipado fuera del sistema. Como consecuencia, el movimiento
está amortiguado, salvo que alguna fuerza externa lo mantenga. Si el
amortiguamiento es mayor que cierto valor crítico, el sistema no oscila,
sino que regresa a la posición de equilibrio. La rapidez con la que se
produce este regreso depende de la magnitud del amortiguamiento, pudiéndose
dar dos casos distintos: el sobreamortiguamiento y el movimiento críticamente
amortiguado. Cuando el amortiguamiento no supera este valor crítico el
sistema realiza un movimiento ligeramente amortiguado, semejante al
movimiento armónico simple, pero con una amplitud que disminuye
exponencialmente con el tiempo.
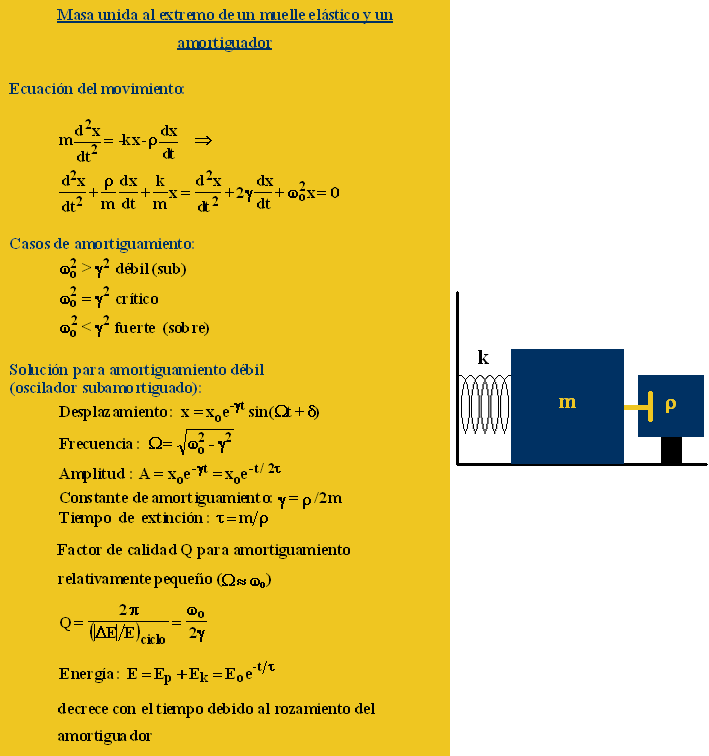
Para
ilustrar este tipo de movimiento consideremos una masa
m unida al extremo de un muelle elástico de constante k, y a un
amortiguador cuya fuerza de fricción es proporcional a la velocidad de la
masa m en cada instante.
|
|
|
|
|
Oscilación
libre
La
característica esencial de una oscilación libre es que la amplitud se
mantiene constante, y por tanto, la energía total se mantiene constante.
En el espacio de las fases (v-x) el móvil describe una elipse.
Instrucciones
Se
introduce la posición inicial y la velocidad inicial del móvil, y después
se pulsa en el botón Empieza.
-
Se
observa la posición del móvil en función del tiempo en la parte
izquierda de la ventana, gráfico x-t. El valor de la posición x del
móvil se muestra en la esquina superior izquierda.
-
La
trayectoria del móvil en el espacio de las fases, gráfico v-x, en la
parte superior derecha.
-
La
energía total del móvil en función del tiempo, gráfica E-t, en la
parte inferior derecha.
|
|
|
|
|
Movimiento
armónico simple
y curvas de energía potencial
En
la siguiente simulación vamos a interpretar gráficamente las
relaciones energéticas mediante la representación de la curva de la
energía potencial de una partícula de masa m unida a un muelle elástico
de constante k. La curva de energía potencial es una parábola de vértice
x = 0. Podemos observar cómo cambian los valores de la energía cinética
(en color rojo) y potencial (en color azul) a medida que se mueve la partícula
a lo largo del eje X. El módulo y el sentido de la fuerza (en color rosa) que actúa
sobre la partícula vienen dados por la pendiente cambiada de signo de la
recta tangente a la curva de energía potencial.
Instrucciones
-
Se
introduce la constante elástica del muelle, en el control de edición
titulado Cte. del muelle, la masa de la partícula se
ha tomado igual a la unidad.
-
Se
introduce la energía total de la partícula, en el control de edición
titulado Energía Total. Se pulsa en el botón
titulado Empieza para comenzar la animación.
-
Se
pulsa el botón titulado Pausa para parar momentáneamente
la animación, y observar los valores de la energía cinética,
potencial y la fuerza sobre la partícula. En particular, observar
dichos valores, cuando la partícula pasa por el origen y por las
posiciones de máximo desplazamiento.
-
Se
pulsa en el mismo botón titulado ahora Continua para
reanudar el movimiento normal. Se pulsa varias veces en el botón
titulado Paso, para acercar la partícula a una
posición concreta.
|
|
Oscilador
amortiguado
La
característica esencial de la oscilación amortiguada es que la amplitud de la
oscilación disminuye exponencialmente con el tiempo. Por tanto, la energía del oscilador
también disminuye. En el espacio de las fases (v-x)
vemos que el móvil describe una espiral que converge hacia el origen.
Si el amortiguamiento
del sistema es grande,
pueden darse las situaciones de sistema críticamente amortiguado y sistema
sobreamortiguado. En ambos casos, no hay oscilaciones y la partícula se aproxima
gradualmente a la posición de equilibrio. El retorno más rápido a la
posición de equilibrio se produce en el amortiguamiento crítico.
Instrucciones
Se introduce la posición inicial y la velocidad inicial del móvil, y la constante de
amortiguamiento, después se pulsa el botón titulado Empieza.
Probar con los siguientes valores de la constante de amortiguamiento: 5
(oscilador amortiguado), 100
(sistema críticamente amortiguado), 110 (sistema sobreamortiguado).
-
Se observa la posición del móvil en función del tiempo en la parte izquierda de la
ventana, gráfico x-t. El valor de la posición x del móvil se muestra
en la esquina superior izquierda.
-
La trayectoria del móvil en el espacio de las fases, gráfico
v-x, en la parte
superior derecha.
-
La energía total del móvil en función del tiempo, gráfica
E-t, en la parte
inferior derecha.
|
|
|
|
|
CUESTIONES
a
En un movimiento armónico simple, existe una relación constante entre la
aceleración y
-
el
período
-
la
velocidad
-
la
elongación
-
la
frecuencia
b
En un movimiento armónico simple, la velocidad es máxima cuando
-
la
elongación es máxima
-
la
aceleración es cero
-
el
período es máximo
-
la
frecuencia es máxima
c
En un movimiento armónico simple, cuando la elongación desde el punto de
equilibrio es máxima
-
la
energía potencial es máxima y la energía cinética es mínima
-
la
energía potencial es un cuarto de la energía cinética
-
la
energía potencial es mínima y la energía cinética es máxima
-
la
energía cinética es un cuarto de la energía potencial
d
Una masa de 10 kg oscila con una amplitud de 20 cm unida a un muelle de
constante elástica 100 N/m. La energía cinética cuando pasa por la
posición de equilibrio es
-
20
J
-
4
J
-
2
J
-
40
J
e
Una masa de 500 g oscila con una amplitud decreciente en el tiempo, unida a un
muelle de constante elástica 125 N/m. Si la mitad de su energía se pierde en
4 s, la pérdida relativa de energía por
ciclo es
-
68.9%
-
89.6%
-
8.96%
-
6.89%
Soluciones: a3
b2 c1 d3 e4
|
|
RECURSOS
MULTIMEDIA Y WEB
Si
desea ampliar sus conocimientos, pueden resultarle útiles los recursos
que se encuentran referenciados en el apartado  del enlace
del enlace 
| |
ENLACES
Si
desea conocer las direcciones y recursos de otras instituciones, pueden
resultarle útiles las referencias que se encuentran en el enlace 
| |