DESCRIPTION

Observing the nature, we realize that many physical processes (for example, the Earth rotation around its polar axis) are repetitive, happening the facts cyclically. In these cases we speak about periodic motion and we characterize it by means of its period, which is the necessary time to complete a cycle, or by its frequency, which represents the number of complete cycles in the unit of time.

An interesting case of periodic motion appears when a physical system oscillates around an equilibrium position. The system describes the same path, first in a sense and then in the opposite one, inverting the motion sense in both ends of the path. A complete cycle includes the crossing of the equilibrium position twice. The mass hanging from a pendulum or a spring, the electrical charge of a condenser, the strings of a musical instrument, and the molecules of a crystalline net are examples of physical systems that often realize oscillatory motion.

The simplest case of oscillating motion is called simple harmonic motion and takes place when the total force on the system is a restoring linear force. Fourier's theorem gives us the reason of its importance: any periodic function may be built from a set of simple harmonic functions.

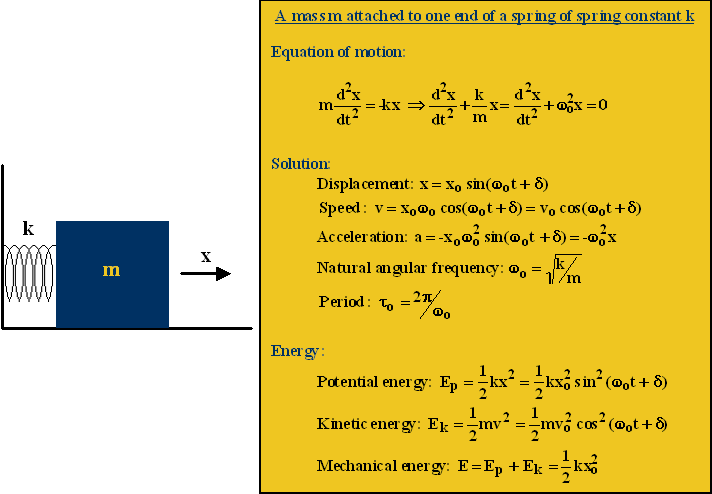
Simple harmonic motion

We take as representative system that describes simple harmonic motion, a mass m hanged from one end of a spring of stiffness constant k, as we can see in the figure (mass-spring system). The other spring end is fixed. The mass horizontal motion can be described using the Newton's second law: the force acting on the mass is the spring restoring force, which is proportional to the displacement from the equilibrium position, x, being its sense opposite to that of x.

Damped oscillator

All real oscillators undergo frictional forces. Frictional forces dissipate energy, transforming work into heat that is removed out of the system. As a consequence, the motion is damped, except if some external force supports it. If the damping is greater than a critical value, the system does not oscillate, but returns to the equilibrium position. The return velocity depends on the damping and we can find two different cases: over damping and critical damping. When the damping is lower than the critical value, the system realizes under damped motion, similar to the simple harmonic motion, but with an amplitude that decreases exponentially with time.

To illustrate this kind of motion, we consider the mass-spring system attached to a dashpot with a drag force proportional to the mass velocity. 

EXAMPLES AND SIMULATIONS

Free oscillation

The essential characteristic of free oscillations is that the amplitude, and therefore, the total energy remain constant. In the phase space (v,x) the mass describes an ellipse.

Instructions

Introduce the initial position and speed of the mass, and then touch the button Empieza.

1. The mass position as a function of time can be observed in the left part of the window, graph x-t. The mass position value x appears in the upper left corner.

2. The mass path in the phase space, graph v-x, can be observed in the upper right part of the window.

3. The mass total energy as a function of time, graph E-t, can be observed in the lower right part of the window.

Simple harmonic motion and potential energy curves

In the following simulation we are going to interpret graphically the energetic relations using the representation of the potential energy curve of the mass-spring system. The potential energy curve is a parabola of vertex in x=0. We can observe how the values of the kinetic energy (in red) and of the potential one (in blue) change when the mass moves along the x-axis. The force module and sense acting on the mass (in pink) can be calculated from the slope of the tangent right to the potential energy curve.

Instructions

1. Introduce the spring stiffness constant, in the button called Cte del muelle.

2. Introduce the total mass energy. To begin the animation, click the button called Empieza.

3. If the button called Pausa is clicked, the animation stops, and we can observe the values of the kinetic and potential energy and total force. As an important case, observe the above-mentioned values when the mass passes through x=0 and the maximum displacement positions.

4. Click the same button (now called Continua) to resume the motion. Click Paso several times, to bring the mass to a definite position.

Damped oscillator

The essential characteristic of damped oscillator is that amplitude diminishes exponentially with time. Therefore, oscillator energy also diminishes. In the phase space (v-x) the mass describes a spiral that converges towards the origin.

If the damping is high, we can obtain critical damping and over damping. In both cases, there are not oscillations and the mass comes to the equilibrium position. The most rapid return to the equilibrium position corresponds to critical damping. 

Instructions

Introduce mass initial position and speed and the damping constant. Click the button called Empieza.

Try the following damping constant values: 5 (underdamped oscillator), 100 (critically damped system) and 110 (overdamped system).

1. The mass position as a function of time can be observed in the left part of the window, graph x-t. The mass position value x appears in the upper left corner.

2. The mass path in the phase space, graph v-x, can be observed in the upper right part of the window.

3. The mass total energy as a function of time, graph E-t, can be observed in the lower right part of the window.

QUESTIONS

a In the simple harmonic motion, there is a relation between mass acceleration and

1. the period                                                                         

2. the speed                                                                           

3. the displacement                                                                             

4. the frequency

b In the simple harmonic motion, velocity has a maximum when

1. displacement has a maximum                                                       

2. acceleration is zero                                                       

3. period has a maximum                                                            

4. frequency has a maximum

c In the simple harmonic motion, when the displacement from equilibrium position has a maximum

1. potential energy has a maximum and kinetic energy a minimum

2. potential energy is a quarter of kinetic energy

3. potential energy has a minimum and kinetic energy a maximum

4. kinetic energy is a quarter of potential energy

d A 10 kg mass oscillates with 20 cm amplitude, hanged from a spring of stiffness constant 100 N/m. When the mass passes trough the equilibrium position, its kinetic energy is

1. 20 J                                                                          

2. 4 J                    

3. 2 J   

4. 40 J

e A 500 g mass oscillates with amplitude that decreases with time, hanged from a spring of stiffness constant 125 N/m. If the mass loses the half of its energy in 4s, the relative energy loss per cycle is 

1. 68.9%                                                            

2. 89.6%                                            

3. 8.96%                                                                

4. 6.89%

  Solutions:  a3   b2   c1   d3   e4  

MULTIMEDIA AND WEB RESOURCES

If you want to extend your study, the resources indexed in the paragraph of the link can be useful for you.